Questões de Estatística

• A.

  R$ 1.825,00

• B.

  R$ 1.805,00

• C.

  R$ 1.710,00

• D.

  R$ 1.695,00

• E.

  R$ 1.650,00

Um banco deseja testar se a produtividade média de um grupo de empregados de determinado setor da agência I é igual à produtividade média de um outro grupo de empregados de um setor equivalente da agência II. A produtividade foi definida em função do número diário de contratos avaliados por cada empregado. Como as duas agências possuem características similares, foram coletadas amostras de igual tamanho (32 empregados), obtendo-se os resultados apresentados na tabela a seguir. Considere que as distribuições das produtividades de ambas as agências sejam normais com variâncias iguais.

Considere ainda que o teste t para a comparação da média de duas amostras independentes tenha sido aplicado. Dado que P(Z > 1,96) = 0,025 e P(Z > 2,326) = 0,01, em que Z é uma distribuição normal padrão, julgue os itens a seguir com base nessas informações.

Sob a hipótese nula, a estatística do teste segue a distribuição t com 31 graus de liberdade.

• C. Certo
• E. Errado

Considere uma variável aleatória contínua X cuja função de distribuição seja dada pela função logística  Com base nessas informações, julgue os itens que se seguem. A variável aleatória X está simetricamente distribuída em torno da sua mediana.

• C. Certo
• E. Errado

NAS QUESTÕES NUMERADAS DE 16 A 40, ASSINALE A ÚNICA ALTERNATIVA QUE RESPONDE CORRETAMENTE AO ENUNCIADO.

Índice calculado mensalmente pela Fundação Getúlio Vargas, com a finalidade de medir o comportamento dos preços em geral da economia brasileira, constituindo-se na média aritmética ponderada de alguns dos principais índices brasileiros:

• A.

  Índice de Preços no Atacado (IPA).

• B.

  Índice Nacional de Preços ao Consumidor (INPC).

• C.

  Índice de Preços ao Consumidor (IPC).

• D.

  Índice Geral de Preços – Disponibilidade Interna (IGP-DI).

Para resolver as questões de números 31 a 33, utilize, dentre as informações dadas a seguir, as que julgar apropriadas.

Se Z tem distribuição normal padrão, então:

P (Z > 2) = 0,023, P (Z < 1,64) = 0,945,

P (0 < Z < 1,5) = 0,433, P (Z < 1,34) = 0,91

Uma corretora de ações, que opera numa certa Bolsa de Valores, faz aplicações financeiras de compra e venda de ações nas áreas Industrial e Comercial, e faz uso de um modelo de probabilidades para a avaliação de seus lucros. O modelo que representa o lucro diário da corretora (em milhares de reais) é dado por:

L = 2 L_I + 3 L_C,

onde

L_I = lucro diário da área Industrial tem distribuição normal com média 5 e variância 16,

L_C = lucro diário da área Comercial tem distribuição normal com média 4 e variância 4.

Supondo independência entre as duas variáveis que compõem L, a probabilidade de um lucro diário superior a 37 mil é

• A. 6,7%
• B. 7,3%
• C. 8,1%
• D. 9,5%
• E. 12,4%

Um banco deseja testar se a produtividade média de um grupo de empregados de determinado setor da agência I é igual à produtividade média de um outro grupo de empregados de um setor equivalente da agência II. A produtividade foi definida em função do número diário de contratos avaliados por cada empregado. Como as duas agências possuem características similares, foram coletadas amostras de igual tamanho (32 empregados), obtendo-se os resultados apresentados na tabela a seguir. Considere que as distribuições das produtividades de ambas as agências sejam normais com variâncias iguais.

Considere ainda que o teste t para a comparação da média de duas amostras independentes tenha sido aplicado. Dado que P(Z > 1,96) = 0,025 e P(Z > 2,326) = 0,01, em que Z é uma distribuição normal padrão, julgue os itens a seguir com base nessas informações.

Para o nível de significância de 2%, há evidências estatísticas suficientemente fortes para se rejeitar a hipótese de que as produtividades médias não são iguais.

• C. Certo
• E. Errado

A temperatura T de destilação do petróleo é uma variável aleatória com distribuição uniforme no intervalo [150, 300]. Seja C o custo para se produzir um galão de petróleo. Determine o lucro esperado por galão, supondo que o preço de venda por galão é uma variável aleatória Y dada por: 

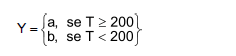
• A. (a + 2b) / 3 − C
• B. (a − C) / 150 + (b − C) / 50
• C. (a + b) / 3 − C
• D. (a + b) / 150 − C
• E. (2a + b) / 3 − C

Um banco deseja testar se a produtividade média de um grupo de empregados de determinado setor da agência I é igual à produtividade média de um outro grupo de empregados de um setor equivalente da agência II. A produtividade foi definida em função do número diário de contratos avaliados por cada empregado. Como as duas agências possuem características similares, foram coletadas amostras de igual tamanho (32 empregados), obtendo-se os resultados apresentados na tabela a seguir. Considere que as distribuições das produtividades de ambas as agências sejam normais com variâncias iguais.

Considere ainda que o teste t para a comparação da média de duas amostras independentes tenha sido aplicado. Dado que P(Z > 1,96) = 0,025 e P(Z > 2,326) = 0,01, em que Z é uma distribuição normal padrão, julgue os itens a seguir com base nessas informações.

O poder do teste é a probabilidade de a hipótese nula ser rejeitada, dado que, na realidade, as médias são iguais.

• C. Certo
• E. Errado

Seja X uma variável aleatória com função densidade de probabilidade dada por:

• A. e^–4
• B. e^–2
• C. e^–1
• D. e^–1/2
• E. 1

Considerando o teste de hipóteses sobre um parâmetro de uma distribuição populacional, assinale a opção correta.

• A.

  A probabilidade de erro do tipo I é a probabilidade de rejeição da hipótese nula quando essa hipótese é, de fato, verdadeira.

• B.

  O nível de significância do teste é dado pela probabilidade de erro do tipo II.

• C.

  A soma da probabilidades de erro do tipo I e da probabilidade de erro do tipo II deve ser sempre igual a um.

• D.

  O poder do teste é definido como 1 - {probabilidade de erro do tipo I}.