Questões de Estatística

Se uma série temporal tem como processo gerador um modelo estacionário, qual dos modelos abaixo serviria para gerar a série, considerando que, em todos os modelos, et é o ruído branco de média zero e variância 1?

• A. Zt = Zt−1 + et − 0,9 et−1
• B. Zt = a + bt + et, onde a e b são constantes positivas
• C. Zt = Zt−1 + et
• D. Zt = 1,7 Zt−1 − 0,7 Zt−2 + et
• E. Zt = 0,4 Zt−1 + 0,5 Zt−2 + et

O fabricante de uma balança de precisão afirma que o desvio padrão das medições dessa balança é de 0,0002 g. Considere que um usuário dessa balança faça um experimento para testar a afirmação do fabricante. Após 8 medições, esse usuário verifica que o desvio padrão amostral foi igual a 0,0005 g. O usuário decide testar a hipótese nula  versus a hipótese alternativa  . Com base nessas informações, julgue os itens a seguir.

Se a hipótese nula for rejeitada em nível de significância de 5%, então o poder do teste será de 95%.

• C. Certo
• E. Errado

Uma empresa de comércio varejista possui um cadastro de clientes, classificados por ordem alfabética, com informações acerca de uma série de variáveis. Ela planeja contatar, por telefone, uma amostra desses clientes para ouvi-los a respeito de uma certa promoção. Para fazer essa pesquisa, decide-se contatar o oitavo cliente do cadastro e, a seguir, o décimo oitavo, o vigésimo oitavo e assim por diante. O tipo de processo de amostragem usado nesse caso é o de amostragem:

• A.

  sistemática;

• B.

  aleatória simples;

• C.

  estratificada com sorteio aleatório;

• D.

  por conglomerados;

• E.

  estratificada em dois estágios.

Considere a distribuição de probabilidades discreta apresentada a seguir.

Analisando-se esses dados, conclui-se que a:

• A. moda desta distribuição é igual a 2.
• B. média da distribuição é igual à moda.
• C. mediana da distribuição é igual a 2.
• D. distribuição é assimétrica.
• E.

  probabilidade do evento "número ímpar" é igual a 50%.

As informações a seguir referem-se às questões de números 54 e 55.

Seja a variável aleatória bidimensional (X, Y), com função densidade de probabilidade conjunta dada por

f(x, y) = x + y, 0 < x < 1, 0 < y < 1

• A. 1/6
• B. 1/8
• C. 1/10
• D. 1/12
• E. 1/16

Uma rede local de computadores é composta por um servidor e 2 (dois) clientes (Z e Y). Registros anteriores indicam que dos pedidos de certo tipo de processamento, cerca de 30% vêm de Z e 70% de Y. Se o pedido não for feito de forma adequada, o processamento apresentará erro. Sabendo-se que 2% dos pedidos feitos por Z e 1% dos feitos por Y apresentam erro, a probabilidade do sistema apresentar erro é

• A.

  5%

• B.

  4,1%

• C.

  3,5%

• D.

  3%

• E.

  1,3%

Seja B o operador translação para o passado (isto é B Zt = Zt−1). Sejam θ, Θ, e φ números reais maiores do que zero e menores do que um e at um processo de ruído branco. Então um modelo do tipo SARIMA (0, 1, 1) × (0, 0, 1)12 é dado por:

• A. (1 − B) Zt = (1 − ΘB12) at−1 + (1 − ΘB12) at
• B. (1 − B) (1 − B12) Zt = (1 − θB)(1− ΘB12) at
• C. (1 − B) (1 − φB) Zt = (1 − ΘB12) at
• D. (1 − B) (1 − B12) Zt = at
• E. (1 − B) Zt = (1 − θB) (1 − ΘB12) at

Com a seguinte função de probabilidade conjunta, onde x assume os valores 0 e 1, e y assume os valores, 1, 2 e 3,

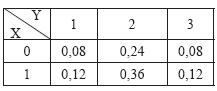
pode-se afirmar que

• A.

  P(Y = 3) = 0,08.

• B.

  P(X =0) = P(Y =2).

• C.

  P(Y = 2 / X = 0) = 0,6.

• D.

  E(X) = 0,4.

• E.

  X e Y são variáveis aleatórias dependentes.

Dois novos tipos de vacina contra determinada doença estão sendo testados: a vacina do tipo A e a vacina do tipo B. Esses dois tipos de vacinas foram aplicados em uma população de voluntários. Sabe-se que 60 % dos voluntários receberam vacina do tipo A e 40% dos voluntários restantes receberam vacina do tipo B. Sabe-se, também, que a vacina do tipo A fornece 70% de imunização e a do tipo B fornece 80% de imunização. Assim, a probabilidade de uma pessoa, escolhida ao acaso, estar imunizada dado que lhe foi aplicada a vacina do tipo A é igual a

• A.

  0,5.

• B.

  0,42.

• C.

  0,68.

• D.

  21/37.

• E.

  42/75.

O Teorema de Bayes diz que, para dois eventos independentes, A e B, com probabilidades não nulas, tem-se que

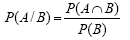
onde, P(A/B) é a probabilidade de ocorrer o evento A, sabendo-se que o evento B já ocorreu. Desse modo pode-se afirmar que

• A.

  se A e B são eventos mutuamente excludentes, então P(A/B) = P(A).

• B.

  se P(B/A) = P(B), então A e B são eventos dependentes.

• C.

  se P(A) ≠ P(B), então A e B são eventos independentes.

• D.

  se P(A) ≠ P(B), então A e B são eventos dependentes.

• E.

  se P(A ∩ B) = 0, então A e B são eventos independentes.