Questões de Estatística do ano 2007

Uma variável aleatória X tem distribuição normal com média μ e desvio padrão σ2. Desejando-se fazer um teste de hipóteses para a média de X do tipo:

com base numa amostra de 100 observações, a região crítica apropriada ao teste, dada em termos da média amostral X , para que a probabilidade de se cometer erro do tipo I seja igual à de se cometer erro do tipo II, é dada por

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Uma urna contém bolas vermelhas e azuis. Para verificar a hipótese de iguais proporções dessas cores, extraem-se 10 dessas bolas, ao acaso e com reposição e observa-se o número de bolas vermelhas obtido. Decide-se aceitar a hipótese acima se este número estiver entre 3 e 7, incluindo o 3 e o 7. Se na amostra selecionada este número foi 9, o nível de significância e o nível descritivo do teste são dados, respectivamente, por:

• A. 7/128 e 11/512
• B. 7/64 e 11/512
• C. 7/64 e 11/1024
• D. 7/128 e 11/1024
• E. 11/1024 e 11/1024

Seja ρ o coeficiente de correlação linear entre duas variáveis aleatórias X e Y e r o coeficiente de correlação amostral, obtido de uma amostra aleatória simples (x1, y1), (x2, y2), ...(xn, yn), da distribuição de (X, Y). Desejando-se testar Ho: ρ = 0 versus Ha: ρ ≠ 0 uma estatística apropriada ao teste e sua distribuição de probabilidades sob Ho são dadas respectivamente por

• A.

  t de Student com (n-1) graus de liberdade.

• B.

  t de Student com (n-2) graus de liberdade.

• C.

   distribuição normal com média zero e variância 1/(n-3).

• D.

   t de Student com (n-2) graus de liberdade.

• E.

  tem distribuição normal com média zero e variância 1/(n-2).

• A. (− ∞, e−1)
• B. (− ∞, −1)
• C. (− ∞, 0)
• D. (− ∞, e−1/2)
• E. (− ∞, −1/2)

O enunciado a seguir refere-se às questões de n^os 63 e 64.

Um pesquisador avaliou se a pressão sangüínea dos candidatos do último Concurso para um Tribunal de Contas se alterava no início da prova. Em condições normais, sem stress, os candidatos entre 18 e 32 anos apresentaram uma pressão sistólica média de 120 mm Hg. Após medir a pressão de 36 candidatos a cinco minutos do início da prova, foi encontrada a pressão sistólica média de 125,2 mm Hg com desvio padrão amostral de 12 mm Hg. Deve-se testar:

Nos níveis de significância de 5% e 10%, é correto afirmar que a(o):

• A. hipótese nula é aceita em ambos os níveis.
• B. hipótese nula é rejeitada em ambos os níveis.
• C. hipótese nula é rejeitada em 5% e aceita em 10%.
• D. hipótese nula é aceita em 5% e rejeitada em 10%.
• E. teste é inconclusivo.

Considere um modelo de regressão linear simples de Y, expressa em 10.000 habitantes, em X, expressa em US$. Suponha que você queira mudar a escala de X para reais ao câmbio de US$ 1= R$ 2,00, mas deixando Y na escala original. Qual será a repercussão dessa mudança para os valores 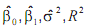 e para o valor da estatística t do teste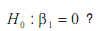

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Em problemas de teste de hipóteses, o nível de significância de um teste pode ser definido como:

• A.

  a máxima probabilidade admitida de se rejeitar a hipótese nula, dado que a hipótese nula é verdadeira;

• B.

  a máxima probabilidade admitida de se rejeitar a hipótese nula, dado que a hipótese nula é falsa;

• C.

  a mínima probabilidade admitida de se rejeitar a hipótese alternativa, dado que a hipótese nula é verdadeira;

• D.

  a mínima probabilidade admitida de se rejeitar a hipótese nula, dado que a hipótese nula é verdadeira;

• E.

  a mínima probabilidade admitida de se rejeitar a hipótese nula, dado que a hipótese alternativa é verdadeira.

A tabela a seguir dá os valores de pares de observações (x_i, y_i ).

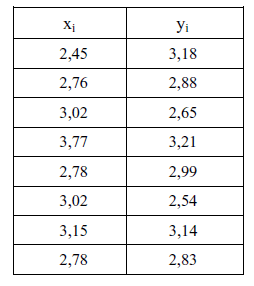
Para testar uma hipótese nula de que não há diferença entre as médias referentes à população X e à população Y, podemos usar o teste dos postos com sinal de Wilcoxon. O valor da estatística de teste para os dados apresentados pode ser:

• A.

  12

• B.

  14

• C.

  19

• D.

  24

• E.

  27

Deseja-se testar H₀: p = 1/2 contra H₁: p = 2/3, em que p é uma proporção populacional de "sucessos", com base numa amostra aleatória simples de tamanho 5 e com o critério que rejeita a hipótese nula de a proporção de "sucessos" na amostra for maior do que 70%. A probabilidade de se cometer erro tipo I com esse critério é:

• A.

  5/36;

• B.

  7/36;

• C.

  3/16;

• D.

  11/16;

• E.

  25/36.

Uma amostra aleatória simples de tamanho 100 será obtida de uma população normalmente distribuída com média μ desconhecida e variância 25. Para testar H0: μ ≥ 100 versus H1: μ < 100, o teste uniformemente mais poderoso de tamanho 0,05 rejeitará H0 se o valor da média amostral for:

• A.

  menor ou igual a 99,18;

• B.

  menor ou igual a 98,25;

• C.

  maior ou igual a 102,34;

• D.

  maior ou igual a 103,28;

• E.

  menor ou igual a 97,26.