Questões de Estatística do ano 2011

Considere que um indicador de acessos — Z(t) — a determinado portal da Internet no dia t siga um processo na forma Z(t) = 0,8 Z(t – 1) + a(t), em que t = 1, 2, 3, ...; a(t) é um ruído branco gaussiano e Z(0) ~ N(0, 1). Com base nessas informações, julgue os itens que se seguem.

O gráfico a seguir representa corretamente a função de autocorrelação do processo Z(t).

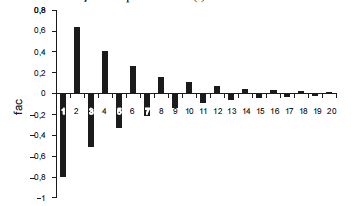
• C. Certo
• E. Errado

Considere que um indicador de acessos — Z(t) — a determinado portal da Internet no dia t siga um processo na forma Z(t) = 0,8 Z(t – 1) + a(t), em que t = 1, 2, 3, ...; a(t) é um ruído branco gaussiano e Z(0) ~ N(0, 1). Com base nessas informações, julgue os itens que se seguem.

Tal modelo é um caso particular do modelo de filtro linear com entrada a(t), saída Z(t) e função de transferência Y(B), ou, equivalentemente, Z(t) = Y(B)a(t), em que Y(B) = 1 + 0,8 B + 0,82 B2 + 0,83B3+..., e B é o operador de translação para o passado tal que BZ(t) = Z(t – 1).

• C. Certo
• E. Errado

Considere que um indicador de acessos — Z(t) — a determinado portal da Internet no dia t siga um processo na forma Z(t) = 0,8 Z(t – 1) + a(t), em que t = 1, 2, 3, ...; a(t) é um ruído branco gaussiano e Z(0) ~ N(0, 1). Com base nessas informações, julgue os itens que se seguem.

Para modelar outro indicador, considere que seja proposto um modelo na forma X(t) = m + Y(B)a(t), em que t = 1, 2, 3, ...; Y(B) = 1 + Y1 B + Y2 B2 + Y3B3+...; em que Yk é uma constante real, B é o operador de translação para o passado tal que BX(t) = X(t – 1) e m é uma constante real. Com base nessas informações, é correto afirmar que X(t) segue um processo de médias móveis, e, portanto, é estacionário em torno da média m.

• C. Certo
• E. Errado

Considere que um indicador de acessos — Z(t) — a determinado portal da Internet no dia t siga um processo na forma Z(t) = 0,8 Z(t – 1) + a(t), em que t = 1, 2, 3, ...; a(t) é um ruído branco gaussiano e Z(0) ~ N(0, 1). Com base nessas informações, julgue os itens que se seguem.

Tal processo corresponde a um modelo autorregressivo de ordem 0,8.

• C. Certo
• E. Errado

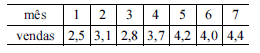
Considerando a série temporal mostrada acima, correspondente à evolução mensal das vendas de certo produto, julgue os itens subsecutivos, acerca de séries temporais.

Para a série mostrada, as médias móveis de ordem 3 são 2,8; 3,2; 3,8; 3,966; 4,2.

• C. Certo
• E. Errado

Seja uma curva de frequência de uma distribuição estatística unimodal caracterizando uma curva leptocúrtica. É correto afirmar que nesta distribuição

• A.

  a moda é menor que a mediana e a mediana menor que a média.

• B.

  a média é menor que a mediana e a mediana menor que a moda.

• C.

  a curva apresenta uma cauda mais acentuada à direita.

• D.

  os dados estão fracamente concentrados em torno da moda, apresentando uma curva fracamente afilada.

• E.

  os dados estão fortemente concentrados em torno da moda, apresentando uma curva bastante afilada.

Julgue os itens que se seguem, relativos a curtose.

A distribuição será leptocúrtica se o coeficiente de excesso de curtose for negativo.

• C. Certo
• E. Errado

A menção final Z de cada aluno de determinada turma será calculada na forma de nota padronizada: Z = (X - m)/s, em que X é a nota bruta desse aluno, m é a média das notas brutas dos alunos da turma e s é o desvio padrão dessas notas. Cada nota padronizada será comparada com os quantis da distribuição normal, de acordo com a tabela abaixo.

Com base nessas informações, julgue os itens de 105 a 108.

Considere que o coeficiente de assimetria da distribuição das notas dos alunos tenha sido igual a 1,80. Nessa situação, as proporções de menções A e B observadas foram menores que as proporções esperadas correspondentes.

• C. Certo
• E. Errado

Considerando as densidades de probabilidade ilustradas na figura acima, julgue os itens que se seguem a respeito dos momentos dessas distribuições.

Se a distribuição B for t de Student, então o seu coeficiente de assimetria será nulo.

• C. Certo
• E. Errado

Considerando as densidades de probabilidade ilustradas na figura acima, julgue os itens que se seguem a respeito dos momentos dessas distribuições.

Se a distribuição de B não for normal, então sua curtose é negativa.

• C. Certo
• E. Errado