Questões sobre Probabilidade

Dado um indivíduo com 50 anos, a probabilidade de morrer antes de completar 55 anos é de, aproximadamente,

• A.

  3,8%

• B.

  4,7%

• C.

  8,8%

• D.

  95,3%

• E.

  96,2%

Segundo a Pesquisa Nacional por Amostra de Domicílios – PNAD-2008, aproximadamente 30% dos domicílios brasileiros possuíam microcomputador, sendo que 22% desses tinham acesso à Internet. Restringindo a população aos domicílios com rendimento mensal superior a 20 salários mínimos (que representavam 5% do total), as porcentagens alteraram para 90% e 80%, respectivamente. Selecionando-se aleatoriamente um domicílio dessa amostra, a renda mensal domiciliar observada foi inferior a 20 salários mínimos; então, a probabilidade de ele possuir microcomputador e ter acesso à Internet é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Seja X uma variável aleatória não negativa do tipo contínuo, tal que F_X(p_0,90) = 0,90. Considere uma amostra aleatória de tamanho n de X. Se X₍₁₎ e X_(n) são as estatísticas de ordem mínimo e máximo da amostra, respectivamente, então 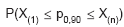é

• A.

  1 − (0,90)ⁿ

• B.

  1 − (0,90)ⁿ − (0,10)ⁿ

• C.

  (0,90)ⁿ

• D.

  (0,90)ⁿ − (0,10)ⁿ

• E.

  (0,90)ⁿ + (0,10)ⁿ

Um comitê é formado por três pesquisadores escolhidos dentre quatro estatísticos e três economistas. A probabilidade de não haver nenhum estatístico é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Em uma empresa, por experiências passadas, sabe-se que a probabilidade de um funcionário novo, o qual tenha feito o curso de capacitação, cumprir sua cota de produção é 0,85, e que essa probabilidade é 0,40 para os funcionários novos que não tenham feito o curso. Se 80% de todos os funcionários novos cursarem as aulas de capacitação, a probabilidade de um funcionário novo cumprir a cota de produção será

• A.

  0,48

• B.

  0,50

• C.

  0,68

• D.

  0,76

• E.

  0,80

O intervalo de tempo entre a chegada de dois navios a um porto, em horas, segue distribuição exponencial com média 1. Se acaba de chegar um navio, qual a probabilidade aproximada de que leve mais de uma hora até a chegada do próximo?

• A.

  0,37

• B.

  0,5

• C.

  0,63

• D.

  0,75

• E.

  0,9

Considere duas variáveis aleatórias X e Y com função de densidade conjunta

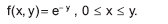
A função de densidade condicional f(x|Y=y) é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Os 100 funcionários de uma empresa receberão, no final de cada mês, uma dentre duas revistas: A ou B. No primeiro mês, a empresa distribuiu ao acaso, entre seus funcionários, 50 revistas A e 50 revistas B e, dias depois, cada funcionário foi solicitado a responder se, no mês seguinte, desejaria receber a mesma revista ou a outra. As respostas foram as seguintes:

- 60% dos que receberam A desejam receber de novo A.

- 40% dos que receberam A desejam receber B no próximo mês.

- 90% dos que receberam B desejam receber de novo B.

- 10% dos que receberam B desejam receber A no próximo mês.

Imaginando que essas respostas sejam as mesmas em todos os meses seguintes, a distribuição das revistas tenderá a uma estabilidade. Quando a estabilidade for atingida, para quantos funcionários a revista A será distribuída?

• A.

  10

• B.

  20

• C.

  30

• D.

  40

• E.

  60

Com base no estudo de distribuições de probabilidade, assinale a alternativa que apresenta a probabilidade de dar 3 caras, ao se lançar 5 vezes uma moeda não viciada.

• A. 29%.
• B. 31%.
• C. 33%.
• D. 34%.
• E. 35%.

Em uma loja, as unidades vendidas por dia de um determinado eletrodoméstico apresentam a seguinte distribuição de probabilidades de ocorrência de venda:

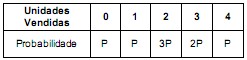
A probabilidade de que em um determinado dia tenham sido vendidas mais que uma unidade do eletrodoméstico é igual a

• A.

  87,5%.

• B.

  80,0%.

• C.

  75,0%.

• D.

  60,0%.

• E.

  50,0%.