Questões sobre Probabilidade

Suponha que o número de partículas emitidas por uma fonte radioativa durante um período de tempo t seja uma variável aleatória com distribuição de Poisson. Sabe-se que a probabilidade de que não haja emissões durante o tempo t é 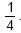 . A probabilidade de que haja pelo menos duas emissões durante o tempo t é

• A.

  ln4 − 1

• B.

  

• C.

  

• D.

  

• E.

  

Se X é uma variável aleatória com distribuição binomial com parâmetros n e p, sua função geratriz de momentos é dada por

• A.

  

• B.

  

• C.
• D.

  

• E.

  

Considere amostras ordenadas de tamanho 4 com repetição, com escolhas aleatórias tomadas de uma população de tamanho 10. A probabilidade de que nenhum elemento apareça mais de uma vez na amostra é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Considere uma sequência de ensaios de Bernoulli independentes com probabilidade de sucesso igual a 0,4. O número esperado de ensaios para que se obtenha o segundo sucesso é

• A.

  20

• B.

  16

• C.

  10

• D.

  8

• E.

  5

Uma urna contém n bolas numeradas de 1 até n. Duas bolas são retiradas ao acaso e com reposição. Seja X a variável aleatória que representa o valor da diferença absoluta entre os dois números observados. A probabilidade de X ser igual a um é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Suponha que se realiza cinco ensaios independentes todos com probabilidade de sucesso igual a 0,3. Seja X a variável aleatória que representa o número de sucessos nesses cinco ensaios e seja Y a variável aleatória que representa o número de sucessos nos três primeiros ensaios. Nessas condições, a probabilidade de Y ser igual a dois, dado que X assumiu o valor três, é igual a

• A.

  

• B.

  

• C.

  

• D.
• E.

  

Considere uma sequência de ensaios de Bernoulli, independentes, e onde a probabilidade de sucesso é p. Seja X o número de ensaios necessários até a ocorrência do primeiro sucesso. Suponha que em quatro repetições desse experimento observou-se para X os valores: 1, 3, 2, 4. O estimador de máxima verossimilhança de p, baseado nesta amostra, é

• A.

  0,8

• B.

  0,5

• C.

  0,4

• D.

  0,3

• E.

  0,2

Uma variável aleatória X apresenta uma média igual a 100. Sabe-se que pelo Teorema de Tchebyshev a probabilidade mínima de que X pertença ao intervalo (80 , 120) é igual a 84%. A variância de X é igual a

• A.

  25.

• B.

  64.

• C.

  256.

• D.

  324.

• E.

  400.

Considerando que, de uma urna que contém 3 bolas amarelas, 5 bolas brancas e 4 bolas vermelhas, 6 bolas sejam escolhidas aleatoriamente, sem reposição, assinale a opção correta.

• A. A probabilidade de que a escolha contenha duas bolas de cada cor é maior que 20%.
• B. A probabilidade de que a escolha não contenha bolas brancas é maior que 1%.
• C. O número esperado de bolas vermelhas na escolha é igual a 4.
• D. A probabilidade de que o número de bolas vermelhas na escolha seja igual ao número de bolas brancas é de 5/21.
• E. A probabilidade de que a escolha contenha todas as 5 bolas brancas é maior que 1%.

Seja a distribuição binomial 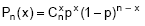 com parâmetro p desconhecido e x o número de ocorrências de um determinado acontecimento em n provas independentes. Se em 6 provas independentes o acontecimento A ocorreu 3 vezes e em 10 provas independentes o acontecimento A ocorreu 4 vezes, então a estimativa de p pelo método da máxima verossimilhança é

• A.

  45,00%.

• B.

  43,75%.

• C.

  42,00%.

• D.

  40,25%.

• E.

  40,00%.