Questões de Estatística da Fundação CESGRANRIO (CESGRANRIO)

Deseja-se utilizar o teste do sinal em uma amostra para testar se a mediana populacional é igual a 40. Se todos os valores da amostra forem superiores a 40, então o valor de P estará próximo de

• A.

  0

• B.

  0,25

• C.

  0,50

• D.

  0,75

• E.

  1

Considere uma distribuição conjunta de probabilidades, contínua e uniforme sobre o círculo de raio 1, centrado no ponto (1, 1), como mostra o gráfico abaixo. O gráfico também mostra dois outros círculos, A e B, centrados em (1, 1) e com raios de 0,25 e 0,5, respectivamente.

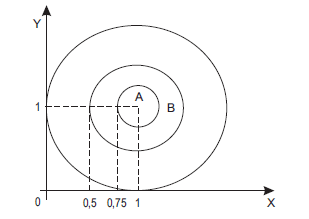
A probabilidade de que um ponto (X, Y) pertença a A, dado que pertence a B, é

• A.

  3/5

• B.

  1/2

• C.

  1/3

• D.

  1/4

• E.

  1/5

Para comparar médias de vários tratamentos em uma população que não siga distribuição normal, o teste adequado é o

• A.

  do sinal

• B.

  Kolmogorov-Smirnov

• C.

  Kruskal-Wallis

• D.

  teste de Wilcoxon

• E.

  t-student

Quando se lança uma certa moeda, a probabilidade de o resultado ser cara é p. A moeda foi lançada dez vezes, sucessivas e independentes, e o resultado foi de 2 caras e 8 coroas. Tendo em vista este experimento, a estimativa de máxima verossimilhança de p é

• A.

  0.2

• B.

  0.25

• C.

  0.3

• D.

  0.35

• E.

  0.4

Considere o plano em blocos completos aleatorizados, com resposta dada por Y_ij, onde o índice i se refere ao i-ésimo tratamento e o índice j se refere ao j-ésimo bloco, com i = 1,2,...,t e j = 1,2,...,b. Com respeito a tal plano, analise as afirmativas abaixo.

I - As variáveis aleatórias Y_ij são independentes e identicamente distribuídas.

II - A soma de quadrados de tratamentos é sempre menor em comparação ao experimento não considerando blocagem.

III - O quadrado médio de tratamentos é sempre menor em comparação ao experimento não considerando blocagem.

IV - A estimativa da variância do erro, dada pelo quadrado médio do erro, é sempre menor em comparação ao experimento não considerando blocagem.

Está correto APENAS o que se afirma em

• A.

  I

• B.

  II

• C.

  I e II

• D.

  II e IV

• E.

  III e IV

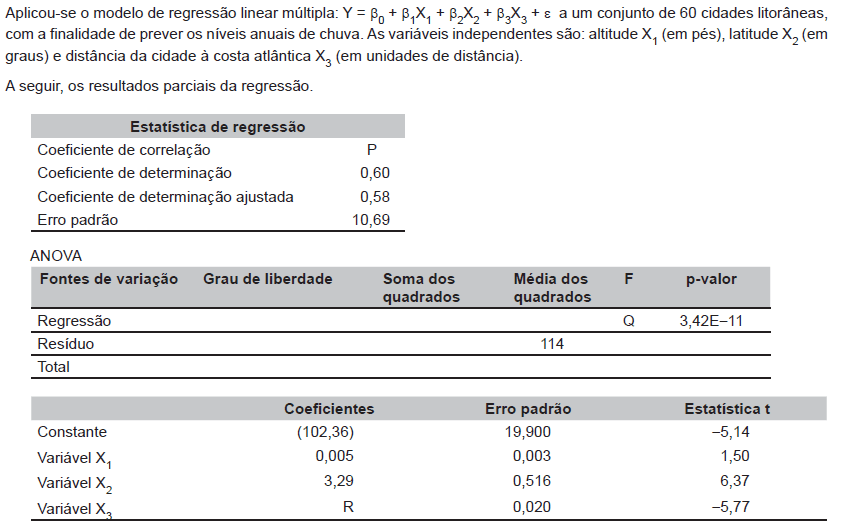
Os valores de P, Q e R são respectiva e aproximadamente iguais a

• A.

  0,4, 28 e 0,2

• B.

  0,4, 84 e −0,2

• C.

  0,8, 28 e 0,1

• D.

  0,8, 28 e −0,1

• E.

  0,8, 84 e 0,1

Dois vetores, v1 e v2, armazenam N inteiros cada um, estão ordenados de forma crescente e têm a propriedade de que o último elemento de v1 (v1[N−1]) é menor que o primeiro elemento de v2 (v2[0]). É retirado um elemento de cada vez de cada um desses vetores alternadamente, e cada elemento retirado é colocado em uma fila. Posteriormente, os elementos são retirados da fila e inseridos em uma árvore binária de busca. A árvore é percorrida em ordem simétrica, e os elementos são inseridos, assim que retirados, em uma pilha. Depois, cada elemento é retirado da pilha e inserido alternadamente em um dos vetores, começando por v1. Diante do exposto, conclui-se que

• A.

  

• B.

  

• C.

  

• D.

  as listas não estão mais ordenadas.

• E.

  todos os elementos de v1 estão armazenados em v2 e vice-versa.

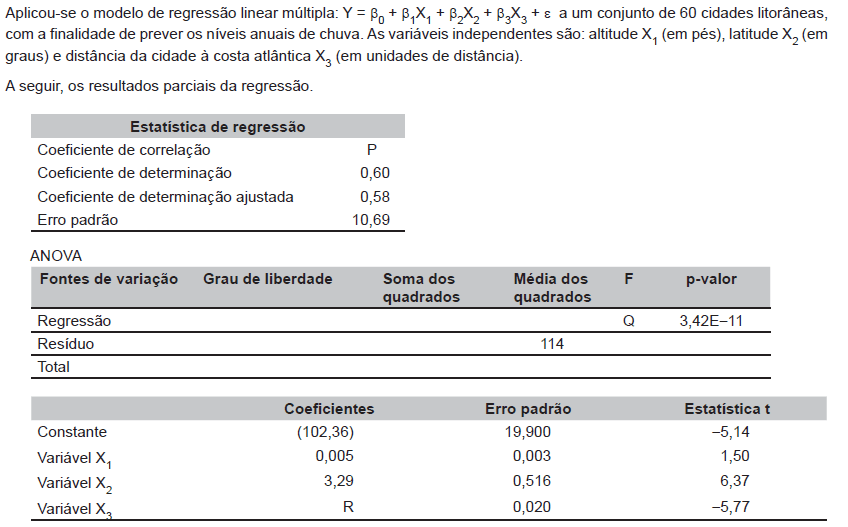
Com base nos resultados apresentados, pode-se afirmar que

• A.

  apenas β₁ não é significativo ao nível de 5%

• B.

  apenas β₂ não é significativo ao nível de 5%

• C.

  apenas β₃ não é significativo ao nível de 5%

• D.

  nenhum coeficiente é significativo ao nível de 5%

• E.

  todos os coeficientes são significativos ao nível de 5%

Ajustou-se um modelo de regressão linear simples a 42 dados. O coeficiente de determinação foi 0,75 e

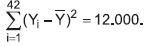
A variância residual é

• A.

  0,87

• B.

  75

• C.

  225

• D.

  285,71

• E.

  292,68

A probabilidade de que ocorra o evento X, dado que o evento Y ocorreu, é positiva e representada por P(X/Y). Similarmente, a probabilidade de que ocorra Y, dado que X ocorreu, é representada por P(Y/X). Se P(X/Y) = P(Y/X), os eventos X e Y são

• A.

  ortogonais

• B.

  coincidentes

• C.

  independentes

• D.

  igualmente prováveis>

• E.

  mutuamente exclusivos