Questões de Estatística da Fundação CESGRANRIO (CESGRANRIO)

Suponha que o custo de produção de energia por kilowatt/hora seja uma função linear do custo do carvão, em centavos de dólar por milhão de Btu. Os resultados parciais a seguir foram obtidos a partir da produção de 12 moinhos.

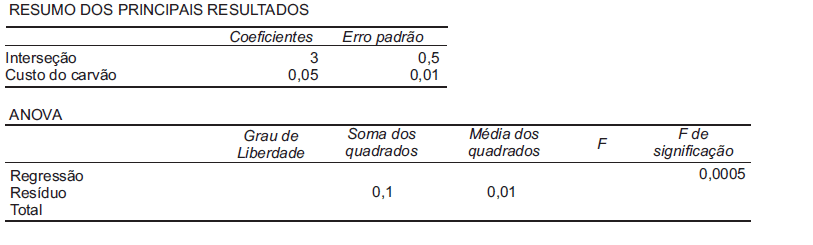
Nesse modelo de regressão linear simples, o coeficiente de determinação que representa o quanto da variável dependente é explicada pela variável independente é

• A.
• B.
• C.
• D.
• E.

A partir desses dados , conclui-se que os resíduos do modelo

• A. seguem o comportamento de um ruído branco.
• B. não seguem o comportamento de um ruído branco, apresentando valor anormal no lag 6.
• C. não seguem o comportamento de um ruído branco, apresentando valores anormais nos lags 6 e 10.
• D. não seguem o comportamento de um ruído branco, apresentando valores anormais nos lags 6, 10 e 16.
• E. não seguem o comportamento de um ruído branco, apresentando valores anormais nos lags 6, 7, 10 e 16.

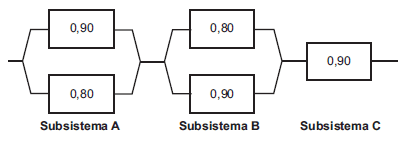
Considere o diagrama acima, formado por três subsistemas, representando a estrutura operacional de um sistema eletrônico. A probabilidade de cada componente operar adequadamente está explicitada no diagrama. Para que o sistema funcione, é necessário que o subsistema C e pelo menos um dos componentes de cada um dos subsistemas A e B funcionem. Supondo-se que os componentes operem de forma independente, a probabilidade de que o sistema funcione é

• A. (0,9) • (0,98)²
• B. (0,9) • (0,98) • (0,97)
• C. 1 − (0,9) • (0,97)²
• D. (0,85)² • (0,9)
• E. 1 − (0,9) • (0,98)²

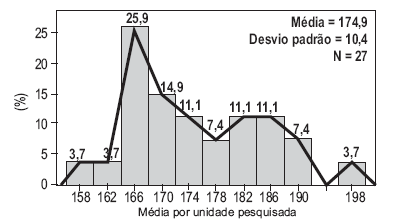
Considerando as informações estatísticas apresentadas no histograma, conclui-se que o(a)

• A.

  número de unidades pesquisadas com médias acima de 176 é 7,4.

• B.

  número de unidades pesquisadas com média igual a 174,9 é 27.

• C.

  número total de unidades pesquisadas é 25.

• D.

  percentual no intervalo (Média ± 2 DP) é 84,1.

• E.

  classe modal desta distribuição tem como limites 164-168.

No último mês, Alípio fez apenas 8 ligações de seu telefone celular cujas durações, em minutos, estão apresentadas no rol abaixo.

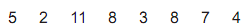
O valor aproximado do desvio padrão desse conjunto de tempos, em minutos, é

• A.

  3,1

• B.

  2,8

• C.

  2,5

• D.

  2,2

• E.

  2,0

O salário médio nacional dos trabalhadores de certa categoria é igual a 4 salários mínimos, com desvio padrão de 0,8 salários mínimos. Uma amostra de 25 trabalhadores
dessa categoria é escolhida ao acaso em um mesmo estado da União. O salário médio da amostra é de 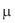   salários mínimos. Deseja-se testar com nível de significância
igual a 10%

Está(ão) correta(s) APENAS a(s) afirmativa(s)

• A.

  I.

• B.

  II.

• C.

  III.

• D.

  I e II.

• E.

  I e III.

O gráfico abaixo mostra uma distribuição de probabilidades discreta sobre os números 1, 2, 3.

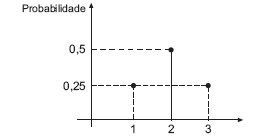
Considerando o gráfico, afirma-se que

• A. a média da distribuição é 0,5.
• B. a média da distribuição é 2.
• C. o desvio padrão da distribuição é maior que 1.
• D. é uma distribuição assimétrica.
• E. é uma distribuição bimodal.

A probabilidade de que, no lançamento de três dados comuns, honestos, a soma dos resultados seja igual a 18 é

• A.

  1/12

• B.

  1/36

• C.

  1/216

• D.

  3/18

• E.

  3/216

Um casal decide ter filhos até que, eventualmente, tenham filhos dos dois sexos, ou seja, uma menina e um menino, não importando a ordem de nascimento. Alcançado este objetivo, não terão mais filhos. Supõe-se que, em cada nascimento, a probabilidade de ser menino seja 50% e de ser menina também 50%, independente do resultado de outros nascimentos, desconsiderando as demais possibilidades, como: não engravidar, gravidez acidental, nascimento de gêmeos, etc. Qual seria o número de filhos mais provável do casal, isto é, a moda da distribuição de probabilidades sobre o número de filhos?

• A. 1
• B. 2
• C. 3
• D. 4
• E. 5

Um pesquisador deseja testar se a renda do filho primogênito é maior que a renda média de seus irmãos. Formula a hipótese nula Ho de que a diferença de rendas (d) = 0 e a hipótese alternativa H1 , d > 0, isto é, a de que a renda do primogênito seja maior que a média das rendas dos irmãos. Desse modo, o(a)

• A. erro do tipo I consiste em aceitar Ho se Ho for falsa.
• B. erro do tipo II consiste em rejeitar Ho se Ho for verdadeira.
• C. poder do teste diminui com o tamanho da amostra.
• D. probabilidade do erro do tipo II é igual a (1 – poder do teste).
• E. probabilidade do erro do tipo II ou do tipo I é chamada de nível de significância do teste.