Questões de Estatística da Fundação CESGRANRIO (CESGRANRIO)

As medidas de dispersão estatísticas servem para comparar a variabilidade em diversos conjuntos de dados que possuem médias bem diferentes. Assim, o coeficiente de variação é uma medida melhor, indicando a variação relativa, e pode ser obtido dividindo-se o desvio padrão pela

• A.

  moda.

• B.

  mediana.

• C.

  escala nominal.

• D.

  média da distribuição.

• E.

  distribuição dos dados

Considere as asserções a seguir. Quanto menor o coeficiente de variação percentual, mais os dados estão concentrados em torno da média.

PORQUE

O coeficiente de variação percentual é inversamente proporcional ao desvio padrão do conjunto de dados.

Analisando-se as asserções, conclui-se que

• A.

  Considere as asserções a seguir. Quanto menor o coeficiente de variação percentual, mais os dados estão concentrados em torno da média. PORQUE O coeficiente de variação percentual é inversamente proporcional ao desvio padrão do conjunto de dados. Analisando-se as asserções, conclui-se que

• B.

  as duas asserções são verdadeiras, e a segunda não é uma justificativa correta da primeira.

• C.

  a primeira asserção é verdadeira, e a segunda é falsa.

• D.

  a primeira asserção é falsa, e a segunda é verdadeira.

• E.

  a primeira e a segunda asserções são falsas.

As questões de n^os 53 a 55 referem-se aos diagramas de dispersão a seguir.

A formulação adequada para o teste de hipótese de existência de relação linear entre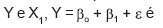

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

As questões de n^os 53 a 55 referem-se aos diagramas de dispersão a seguir.

Se as variáveis Y e X ₁ forem transformadas, respectivamente, para Y ₁ = −2Y + 0,5 e X' ₁=−X ₁+ 0,5, o coeficiente de correlação entre Y ₁ e X' ₁ será

• A.

  0,382

• B.

  0,059

• C.

  -0,059

• D.

  -0,118

• E.

  -0,382

Em estatística, quando dispomos de uma tabela primitiva ou de um rol, precisamos estabelecer a quantidade e o intervalo das classes que vamos criar, pois, de outro modo a distribuição de freqüência pode não ser útil para a análise. Uma das maneiras de determinar o número de classes é usar a(o)

• A.

  porcentagem.

• B.

  Regra de Sturges.

• C.

  amplitude amostral.

• D.

  desvio padrão

• E.

  ponto médio de uma classe.

Considere as asserções a seguir. Em distribuições assimétricas à direita, a mediana é sempre maior do que a média.

PORQUE

Em distribuições com assimetria positiva, a média é afetada por valores extremos.

Analisando-se as asserções, conclui-se que

• A.

  as duas asserções são verdadeiras, e a segunda é uma justificativa correta da primeira.

• B.

  as duas asserções são verdadeiras, e a segunda não é uma justificativa correta da primeira.

• C.

  a primeira asserção é verdadeira, e a segunda é falsa.

• D.

  a primeira asserção é falsa, e a segunda é verdadeira.

• E.

  a primeira e a segunda asserções são falsas.

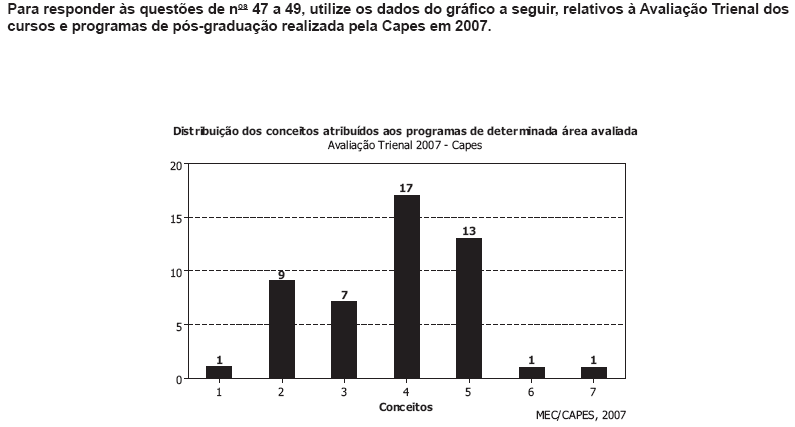O número total de programas, na área, avaliados pela Capes foi

• A. 7
• B. 17
• C. 20
• D. 49
• E. 68

As questões de n^os 53 a 55 referem-se aos diagramas de dispersão a seguir.

O teste de hipótese de que a correlação linear entre Y e X₁ é nula apresentou um valor descritivo (p-value) de 0,480. Conclui-se, então, que

I - a hipótese que 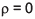 para qualquer nível de significância menor do que 0,480 não deve ser rejeitada;

II - o coeficiente de determinação é menor do que 4,0%;

III - com 48,0% de confiança afirma-se que a relação entre Y e X1 existe, mas é não linear;

IV- a variável Y não deve ser expressa como uma função linear da variável X1.

São corretas APENAS as afirmações

• A.

  I e II

• B.

  III e IV

• C.

  I, II e III

• D.

  I, III e IV

• E.

  II, III e IV

O desvio padrão, a média e a moda, respectivamente, são medidas de:

• A.

  dispersão, tendência e dispersão.

• B.

  dispersão, tendência e tendência.

• C.

  tendência, dispersão e tendência.

• D.

  tendência, tendência e dispersão.

• E.

  tendência, dispersão e dispersão.

Um Banco apresentou, ao final do primeiro trimestre de 2007, o seguinte gráfico sobre a inadimplência de seus clientes:

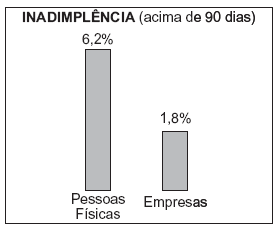
Considere que 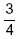 dos clientes desse Banco são empresas e 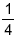, pessoas físicas. Tendo em vista o total de clientes, qual foi, no primeiro trimestre de 2007, o percentual médio de inadimplência?

• A. 2,9%
• B. 3,1%
• C. 3,3%
• D. 3,6%
• E. 4,0%