Questões de Estatística da Escola de Administração Fazendária (ESAF)

Assinale a opção correta.

Segundo as funções biométricas, a formulação da probabilidade de uma pessoa de 50 anos falecer até os 60 anos é dada por:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

O prêmio puro mensal, a ser pago no início de cada mês e no prazo máximo possível (e atuarialmente recomendado), por uma pessoa de 20 anos, que deseje deixar R$ 12.000,00, caso sua morte ocorra até os 65 anos, é dado pela seguinte formulação:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Assinale a opção correta.

Sendo "x" a idade do marido e "y" a idade de sua esposa, a probabilidade do casal estar vivo, após 10 anos é dada por:

Atenção: - observe que nas opções há "x" como idade e como operador matemático (donde a interpretação faz parte da questão).

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Assinale a opção correta.

Se 10Px é igual a 0,85 e 10Py é igual a 0,80, a probabilidade de termos apenas um (1) vivo ao fi nal dos 10 anos é de:

• A.

  = 0,290.

• B.

  = 0,425.

• C.

  = 0,500.

• D.

  = 0,825.

• E.

  = 1,000.

Assinale a opção correta.

Se o 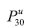  é de R$10.000,00, para um seguro contra morte, imediato e vitalício, e se o segurado deseja pagá-lo no final de cada mês, também de forma imediata e vitalícia, pela metodologia de Woolhouse, teremos a seguinte formulação, para o do respectivo prêmio puro:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

A formulação do 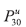 para o recebimento do benefício de R$ 1.000,00, ao fi nal de cada ano, após completar os 65 anos de idade, é dada por:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Para um Benefício de Pensão de R$ 1.000,00, que já esteja sendo recebido no final de cada mês, 80% para o cônjuge e os outros 20% para o filho universitário, sem que haja contribuição futura, a reserva matemática correspondente será obtida por:

Atenção: observe que nas opções há "x" como operador matemático (donde a interpretação faz parte da questão).

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Assinale a opção correta.

O benefício que pagará R$ 1.000,00, no final de cada mês, para a pessoa de 30 anos que atingir os 65 anos, com prêmio (ou contribuição) fracionado no início de cada mês, de forma imediata e durante o período de diferimento do benefício, pelo método prospectiva e antes de atingir a idade de direito ao benefício, terá a formulação da reserva matemática, segundo a metodologia de Woolhouse (tanto para o benefício quanto para o prêmio), dada por:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Seja X uma variável aleatória discreta com função de probabilidade binomial f(x), onde f(x)= C_n,x p^x(1-p)^n-x e C_n,x é o número de combinações de n elementos tomados x a x. Sendo n=6 e p=1/3, determine f(6).

• A.

  1/729.

• B.

  1.

• C.

  0.

• D.

  64/729.

• E.

  8/729.

Sendo F(x) a função de distribuição da variável aleatória definida na questão anterior, determine F(0).

• A.

  0.

• B.

  1/729.

• C.

  64/729.

• D.

  243/729.

• E.

  1.