Questões de Estatística da Escola de Administração Fazendária (ESAF)

Apesar de uma característica numérica supostamente possuir distribuições com variâncias diferentes em duas populações distintas, deseja-se testar a hipótese estatística da igualdade das duas médias. Assim, da primeira população retira-se uma amostra aleatória simples de tamanho 9 e da segunda população retira-se outra amostra aleatória simples independente de tamanho 16. A característica medida na amostra da primeira população tem média 83 e desvio-padrão amostral 7, enquanto a característica medida na amostra da segunda população tem média 81 e desvio-padrão amostral 8. Obtenha o valor mais próximo do erro padrão da diferença estimada entre as médias.

• A.

  1,05.

• B.

  1,92.

• C.

  2,26.

• D.

  2,82.

• E.

  3,07.

Construa um intervalo de 95% de confiança para a média de uma população normal a partir dos dados de uma amostra aleatória simples de tamanho 64 desta população, que forneceu uma média de 48 e um desvio-padrão amostral de 16, considerando que 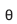 (1,96) = 0,975, onde  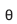 (z) é a função de distribuição de uma variável aleatória normal padrão Z.

• A.

  44,08 a 51,92.

• B.

  41,78 a 54,22.

• C.

  38,2 a 57,8.

• D.

  35,67 a 60,43.

• E.

  32,15 a 63,85.

Seja T um estimador de um parâmetro 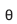 de uma população. Se E(T) =  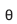, diz-se que T é um estimador de  :

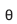• A.

  Eficiente.

• B.

  Não enviesado.

• C.

  Consistente.

• D.

  De mínimos quadrados.

• E.

  De máxima verossimilhança.

Grande parte de uma população de pessoas possui determinada característica. Deseja-se estimar a proporção de pessoas nesta população com esta característica. Qual o valor mais próximo do tamanho de uma amostra aleatória simples para se obter uma estimativa desta proporção na população com um erro padrão de 5%.

• A.

  389.

• B.

  248.

• C.

  156.

• D.

  100.

• E.

  25.

Em determinadas circunstâncias, uma variável aleatória binomial pode ser bem aproximada por uma variável aleatória normal. Seja X uma variável aleatória binomial com n=400 e p=1/2. Calcule o valor mais próximo de  usando a aproximação da variável binomial pela normal, dado que    é a função de distribuição de uma variável aleatória normal padrão Z.

• A.

  0,95.

• B.

  0,97.

• C.

  0,98.

• D.

  0,984.

• E.

  0,99.

Sejam n variáveis aleatórias N(0,1) independentes. A soma de seus quadrados tem uma distribuição de:

• A.

  "t" de Student com n-1 graus de liberdade.

• B.

  "t" de Student com n graus de liberdade.

• C.

  Qui quadrado com n graus de liberdade.

• D.

  Qui quadrado com 2n graus de liberdade.

• E.

  F com 1 grau de liberdade no numerador e n graus de liberdade no denominador.

O cálculo do coeficiente de correlação de postos  de Spearman equivale ao cálculo do coeficiente de correlação linear de Pearson entre duas variáveis usando os postos no lugar dos valores observados, sendo que a fórmula do cálculo do coeficiente de correlação linear de Pearson usando postos se simplifica em  = 1- 6T/(n³ - n) onde T é a soma para todas as observações dos quadrados das diferenças entre os postos de cada observação e n é o número de observações. Assim, calcule o valor mais próximo do coeficiente de correlação de Spearman entre X e Y para a amostra aleatória abaixo de 12 indivíduos onde X e Y medem duas características distintas medidas em cada indivíduo.

X 82 98 87 40 116 113 111 83 85 126 106 117

Y 42 46 39 37 65 88 86 56 62 92 54 81

• A.

  1.

• B.

  0,82.

• C.

  0,45.

• D.

  0,13.

• E.

  -0,59.

Com a seguinte função de probabilidade conjunta, onde x assume os valores 0 e 1, e y assume os valores, 1, 2 e 3,

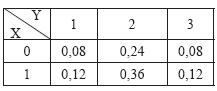
pode-se afirmar que

• A.

  P(Y = 3) = 0,08.

• B.

  P(X =0) = P(Y =2).

• C.

  P(Y = 2 / X = 0) = 0,6.

• D.

  E(X) = 0,4.

• E.

  X e Y são variáveis aleatórias dependentes.

Dois novos tipos de vacina contra determinada doença estão sendo testados: a vacina do tipo A e a vacina do tipo B. Esses dois tipos de vacinas foram aplicados em uma população de voluntários. Sabe-se que 60 % dos voluntários receberam vacina do tipo A e 40% dos voluntários restantes receberam vacina do tipo B. Sabe-se, também, que a vacina do tipo A fornece 70% de imunização e a do tipo B fornece 80% de imunização. Assim, a probabilidade de uma pessoa, escolhida ao acaso, estar imunizada dado que lhe foi aplicada a vacina do tipo A é igual a

• A.

  0,5.

• B.

  0,42.

• C.

  0,68.

• D.

  21/37.

• E.

  42/75.

O Teorema de Bayes diz que, para dois eventos independentes, A e B, com probabilidades não nulas, tem-se que

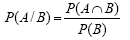
onde, P(A/B) é a probabilidade de ocorrer o evento A, sabendo-se que o evento B já ocorreu. Desse modo pode-se afirmar que

• A.

  se A e B são eventos mutuamente excludentes, então P(A/B) = P(A).

• B.

  se P(B/A) = P(B), então A e B são eventos dependentes.

• C.

  se P(A) ≠ P(B), então A e B são eventos independentes.

• D.

  se P(A) ≠ P(B), então A e B são eventos dependentes.

• E.

  se P(A ∩ B) = 0, então A e B são eventos independentes.