Questões de Estatística da Fundação Carlos Chagas (FCC)

Acerca da Análise Multivariada, considere:

I. Na análise fatorial, o critério varimax é um método de rotação fatorial ortogonal para se conseguir uma estrutura fatorial simplificada.

II. O princípio subjacente da análise de correlação canônica é desenvolver uma combinação linear de cada conjunto de variáveis, dependentes e independentes, visando minimizar a correlação entre os dois conjuntos.

III. A análise de correspondência acomoda tanto dados não métricos quanto relações não lineares.

IV. A análise discriminante é apropriada quando a variável dependente é categórica e as variáveis independentes são métricas.

Está correto o que consta APENAS em

• A.

  I e IV.

• B.

  II e III.

• C.

  I, II e III.

• D.

  II e IV.

• E.

  I, III e IV.

• A.

  I e IV.

• B.

  II, III e IV.

• C.

  I.

• D.

  II e III.

• E.

  I, II e IV.

Dentre os processos, solicitando deferimento, que chegaram em um determinado mês a um tribunal regional de trabalho do estado P, 20%, 25%, 40% e 15% vêm das cidades A, B, C e D, respectivamente. Foram deferidos 30%, 40%, 50% e 20% dos processos, respectivamente, de A, B, C e D. Selecionando-se um processo ao acaso, a probabilidade dele ter vindo da cidade D, sabendo que o mesmo não foi deferido, é igual a

• A.

  12/61.

• B.

  15/61.

• C.

  6/31.

• D.

  6/35.

• E.

  11/60.

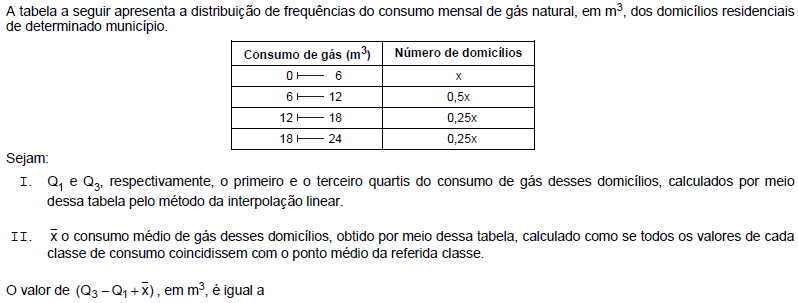
• A.

  15,25.

• B.

  12,50.

• C.

  12,75.

• D.

  10,75.

• E.

  17,25.

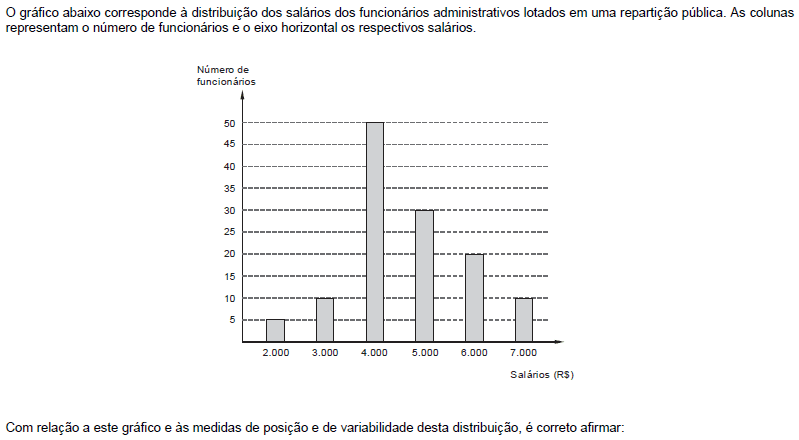
• A.

  Os valores da média aritmética, da mediana e da moda dos salários dos funcionários são iguais.

• B.

  60% dos funcionários ganham acima do valor da moda.

• C.

  15% dos funcionários ganham menos que o valor da mediana.

• D.

  Concedendo um abono fixo no valor de R$ 500,00 para todos os empregados, a correspondente nova média aritmética fica aumentada de R$ 500,00 e a nova variância permanece inalterada.

• E.

  Concedendo um reajuste de 10% a todos os funcionários, a correspondente nova média aritmética fica multiplicada por 1,10 e o novo desvio padrão fica multiplicado por 1,21.

O número de processos com uma determinada característica autuados por dia em um órgão público é considerado como uma variável aleatória X com distribuição de Poisson com média λ. Considere que P(X = 2) = 3 . P(X = 4), e⁻¹ = 0,37, e⁻² = 0,14, e⁻³ = 0,05 e e⁻⁴ = 0,02, em que P(X = k) é a probabilidade de X ser igual a k e e a base dos logaritmos neperianos. A probabilidade de que pelo menos 2 processos sejam autuados em um determinado dia é igual a

• A.

  95%.

• B.

  90%.

• C.

  80%.

• D.

  63%.

• E.

  58%.

• A.

  R$ 3.592,20.

• B.

  R$ 3.444,00.

• C.

  R$ 3.342,00.

• D.

  R$ 3.332,00.

• E.

  R$ 3.264,00.

Uma população, considerada de tamanho infinito, formada pelas alturas dos habitantes de uma cidade é normalmente distribuída com média μ e variância populacional igual a 225 cm². Deseja-se saber, a um determinado nível de significância, se a altura média dos habitantes da cidade é superior a 170 cm com a formulação das hipóteses H₀: μ = 170 cm (hipótese nula) e H₁: μ > 170 cm (hipótese alternativa). Uma amostra aleatória de tamanho 400 é extraída desta população, obtendo-se uma média amostral igual a 171,5 cm. Considere que na distribuição normal padrão (Z) as probabilidades P(Z > 1,64) = 0,05 e P(Z > 2,33) = 0,01. Com base nesta amostra, tem-se que a hipótese H₀

• A.

  não é rejeitada ao nível de significância de 1% e é rejeitada ao nível de 5%.

• B.

  é rejeitada ao nível de significância de 1%, mas não ao nível de 5%.

• C.

  é rejeitada tanto ao nível de significância de 1% como ao nível de 5%.

• D.

  é rejeitada para qualquer nível de significância inferior a 1%.

• E.

  não é rejeitada para qualquer nível de significância superior a 5%.

Em um estudo envolvendo 20 pares de observações (X_i , Y_i), i = 1, 2, 3, ... , 20, foi observada a existência de uma correlação entre as variáveis X e Y. Desejando-se obter uma relação entre X e Y optou-se pelo modelo linear Y_i = α + βXi + ε_i , em que i é a i-ésima observação, α e β são parâmetros desconhecidos e εi o erro aleatório, com as respectivas hipóteses consideradas para a regressão linear simples. Utilizou-se o método dos mínimos quadrados para obter as estimativas de α e β e as médias encontradas para as observações X_i e Y_i foram 20 e 50, respectivamente. Se a reta, cuja equação foi encontrada pelo método dos mínimos quadrados, passa pelo ponto (35 , 80), então, considerando esta equação, tem-se que

• A.

  o menor valor inteiro encontrado para X, tal que Y > 100, é igual a 46.

• B.

  a previsão de Y para X = 25 é igual a 65.

• C.

  o valor da estimativa encontrado para α é igual a 20.

• D.

  o valor de X, tal que a previsão para Y é igual a 40, é igual a 20.

• E.

  o acréscimo verificado para Y, quando X aumenta de uma unidade, é igual a 10.

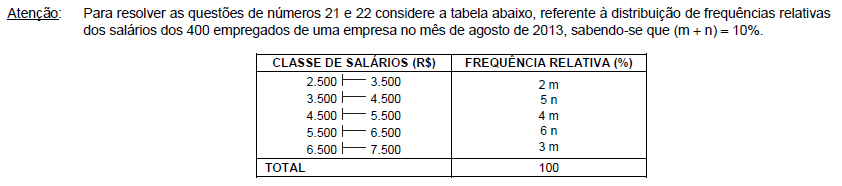O valor da média aritmética dos salários dos empregados foi obtido considerando-se que todos os valores incluídos num intervalo de classe são coincidentes com o ponto médio deste intervalo. O número de empregados correspondente ao intervalo de classe a que pertence o valor da média aritmética é igual a

• A. 80.
• B. 60.
• C. 40.
• D. 100.
• E. 120.