Questões de Estatística da Fundação Carlos Chagas (FCC)

A média geométrica dos números 4, 8 e 16 é

• A.

  maior que a respectiva média aritmética.

• B.

  inferior a 6.

• C.

  igual a 8.

• D.

  igual a 4.

• E.

  superior a 9.

• A. 2 ou − 2.
• B. 1,5 ou −1,5.
• C. 1 ou −1.
• D. 2 ou 1.
• E. 2 ou 1,5.

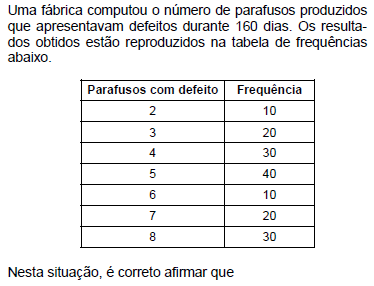
• A.

  a média aritmética dessa distribuição é menor que a mediana.

• B.

  multiplicando o número de parafusos com defeito por dois (2), o desvio padrão da nova distribuição também será multiplicado por dois (2) em relação à distribuição original.

• C.

  a moda dessa distribuição é superior à mediana.

• D.

  dividindo-se pela metade o número de parafusos com defeito, a variância da nova distribuição será dividida pela metade em relação à distribuição original.

• E.

  somando-se dois (2) às frequências da tabela, o desvio padrão e a variância da nova distribuição serão duas unidades maiores em relação aos da distribuição original.

U ma empresa produz componentes de dois tipos: A e B. Sejam as variáveis aleatórias: X = tempo de vida do componente A, em horas e Y = tempo de vida do componente B, em horas. De um lote de 120 componentes do tipo A e 80 componentes do tipo B, retira-se ao acaso um componente. Sabendo-se que X tem distribuição exponencial com média de 1.000 horas e que Y tem distribuição exponencial com média de 700 horas, a probabilidade do componente selecionado ter duração inferior a 1.400 horas é

Dados: e⁻¹ = 0,37; e^−1,4 = 0,25; e⁻² = 0,14

• A. 0,569.
• B. 0,742.
• C. 0,618.
• D. 0,794.
• E. 0,634.

• A. 0,2500.
• B. 0,1600.
• C. 0,0625.
• D. 0,0160.
• E. 0,0250.

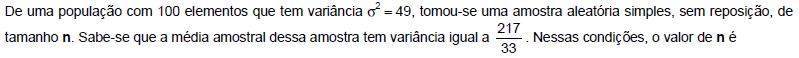
• A. 16.
• B. 49.
• C. 25.
• D. 7.
• E. 10.

• A.
• B. 1.
• C. 1,5.
• D. 1,25.
• E.

Considere as seguintes afirmações:

I. Um gráfico de controle de qualidade é um instrumento que mostra a evolução do nível de operação de um processo pro dutivo e sua variação ao longo de um determinado período.

II. Os limites de um gráfico de controle de qualidade definem a região onde a flutuação é considerada de origem não aleatória.

III. Se não houver pontos fora dos limites superior e inferior de um gráfico de controle de qualidade, considera-se que o pro cesso produtivo está sob controle.

IV. Para a determinação dos limites probabilísticos de um gráfico de controle de qualidade, deve-se conhecer a distribuição de probabilidade da variável aleatória que mede o desempenho do processo.

Está correto o que consta APENAS em

• A. I.
• B. I, III e IV.
• C. III e IV.
• D. I e IV.
• E. II, III e IV.

A função de distribuição acumulada da variável aleatória X, no intervalo [0, 1], é dada por:

F(x) = 3x² − 2x³ .

Se Mo é a moda da variável X, então P (0,2 ≤ X ≤ Mo) é igual a

• A. 0,352.
• B. 0,278.
• C. 0,404.
• D. 0,295.
• E. 0,396.

• A. 1 e 6.
• B. 0,5 e 5.
• C. 1 e 3.
• D. 2 e 5.
• E. 0,5 e 3.