Questões de Estatística da Fundação Carlos Chagas (FCC)

Considere as afirmativas abaixo relativamente a séries temporais.

É correto o que se afirma APENAS em

• A.

  I.

• B.

  I e II.

• C.

  II, III e IV.

• D.

  II e IV.

• E.

  I e IV.

Considere o modelo autorregressivo de ordem dois AR(2) dado por:

Zt = φ1Zt−1 + φ2Zt−2 + at

onde t a é o ruído branco de média zero e variância 2a σ .

Considere as seguintes condições: I. φ1 + φ2 < 1 II. −1< φ1 + φ2 < 1 III. −1< φ2 <1 IV. φ2 − φ1 <1 V. −1< φ1 <1

O processo Zt é estacionário APENAS se satisfaz às condições

• A.

  I, II e III.

• B.

  I, II e V.

• C.

  I, III e IV.

• D.

  I, IV e V.

• E.

  II, III e IV.

Considere as seguintes afirmações:

I. Para um processo ARMA (1, 1) a função de autocorrelação parcial só é diferente de zero no lag 1.

II. Para um processo ARMA (1, 1), onde φ é o coeficiente autoregressivo e θ é o coeficiente de médias móveis, a região de admissibilidade é dada por |φ| < 1 e |θ| < 1.

III. De um modo geral, a análise espectral de séries temporais estacionárias decompõe a série em componentes senoidais com coeficientes aleatórios não-correlacionados.

IV. Um processo ARIMA (1, d ,1), onde d = 1, é estacionário.

Está correto o que se afirma APENAS em

• A.

  I e II.

• B.

  I, II e III.

• C.

  I e III.

• D.

  II e III.

• E.

  II e IV.

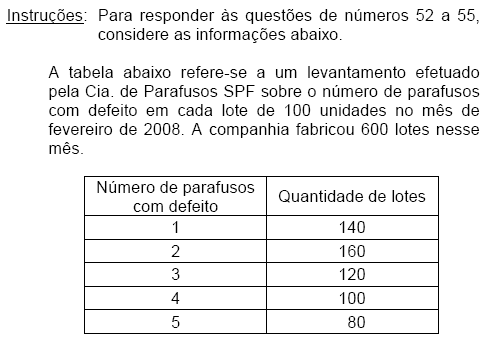
Se multiplicarmos todos os números correspondentes à primeira coluna da tabela por dois, o desvio padrão da nova distribuição será

• A.

  igual ao da anterior.

• B.

  menor que o da anterior.

• C.

  uma vez e meia maior que o da anterior.

• D.

  o dobro da anterior.

• E.

  maior que o dobro da anterior.

Fortes chuvas provocaram enchentes em determinada região do estado, atingindo três cidades A, B e C. A Guarda Municipal do Salvador participou da organização de abrigos para 8 000 desabrigados, coordenada por dois guardas municipais. A tabela abaixo indica como foi feita a distribuição pelos guardas.

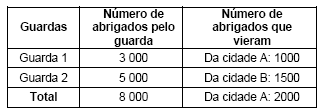
Qual é o número de pessoas da cidade C abrigadas pelo Guarda 2?

• A.

  500

• B.

  1 000

• C.

  1500

• D.

  2000

• E.

  2500

O custo mensal de manutenção C de um aparelho é uma variável aleatória normalmente distribuída com variância populacional igual a 900 (R$)². Para testar a hipótese nula H₀ : μ = R$ 175,00 contra a alternativa H1 : μ ≠ R$175,00 será usada uma amostra de 36 aparelhos (μ é a média da população). Fixando-se o nível de significância (α) em 5%, considerando a população de tamanho infinito e sabendo que na distribuição normal padrão (Z) a probabilidade P(Z > 2) = 2,5%, rejeita-se H₀ caso a média da amostra seja

• A.

  inferior a R$ 167,00.

• B.

  superior a R$ 167,00 e inferior a R$ 187,00.

• C.

  igual a R$ 184,00.

• D.

  superior a R$ 115,00 e inferior a R$ 235,00.

• E.

  inferior a R$ 165,00 ou superior a R$ 185,00.

Um grande fabricante de farinha em uma cidade alega que cada pacote produzido pela sua fábrica não contém menos que 1 kg de farinha. Uma amostra de 16 pacotes apresentou uma média de 0,9 kg e desvio padrão de 0,1 kg. Supondo que a quantidade de farinha em cada pacote tenha uma distribuição normal com média μ e variância desconhecida, deseja-se saber se o fabricante tem razão a um determinado nível de significância α. Seja H₀ a hipótese nula do teste (μ = 1 kg), H₁ a hipótese alternativa (μ < 1 kg) e t_α < 0 o quantil da distribuição t de Student, no nível de significância α, para teste unicaudal com 15 graus de liberdade. Sabendo-se que pelo teste t de Student H₀ foi rejeitada, então

• A.

  tem-se que H₀ seria rejeitada para qualquer nível de significância, pois 0,9 < 1.

• B.

  para um nível de significância β, tal que β > α, H₀ não seria rejeitada.

• C.

  o valor da estatística obtido por meio da amostra para comparação com t_α é igual a − 1.

• D.

  o número de graus de liberdade, no caso, não interfere na obtenção de t_α.

• E.

  

O processo de amostragem que se baseia em dividir a população, desde que possível, em grupos que consistem, todos eles, em indivíduos bastante semelhantes entre si, obtendo a seguir uma amostra aleatória em cada grupo, é denominado

• A.

  Amostragem por conglomerados.

• B.

  Amostragem por estratificação.

• C.

  Amostragem por variabilidade.

• D.

  Amostragem casual simples.

• E.

  Amostragem sistemática.

Dada uma população com n elementos e utilizando o processo da amostragem aleatória simples, sem reposição, consegue-se extrair dessa população um total de 105 amostras de 2 elementos cada uma. Caso tivesse sido adotado o processo com reposição, o número de amostras, também com 2 elementos cada uma, seria de

• A.

  144

• B.

  196

• C.

  225

• D.

  256

• E.

  400

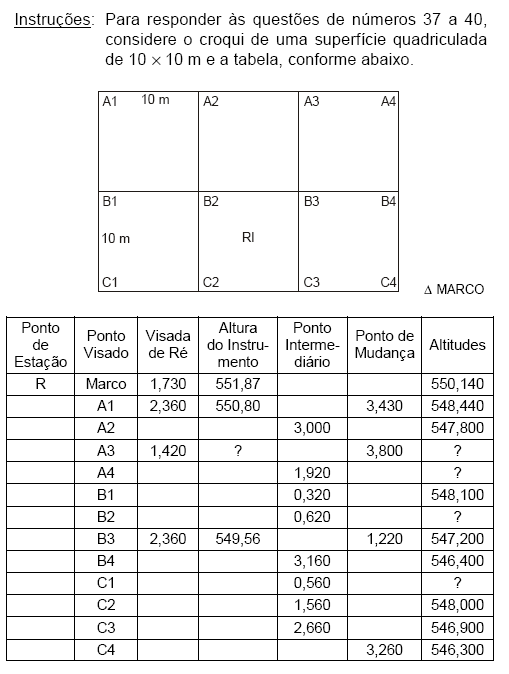
O ponto do terreno de cota mais elevada é equivalente a

• A.

  C1.

• B.

  A1.

• C.

  B3.

• D.

  C2.

• E.

  A3.