Questões de Estatística da Fundação Carlos Chagas (FCC)

Com relação às medidas de assimetria e curtose é correto afirmar que:

• A.

  Uma curva de freqüência de uma distribuição leptocúrtica apresenta necessariamente um coeficiente de assimetria negativo.

• B.

  Uma curva de freqüência de uma distribuição platicúrtica indica que os dados estão fracamente concentrados em torno da moda da distribuição.

• C.

  Uma curva de freqüência de uma distribuição assimétrica à esquerda indica que a moda é inferior à média aritmética.

• D.

  O coeficiente de curtose de uma distribuição de freqüências é sempre positivo, independentemente do método utilizado para o cálculo.

• E.

  Em uma curva de freqüência de uma distribuição leptocúrtica o valor da média é superior ao valor da moda.

Um importante indicador na avaliação da demanda por transporte coletivo é a sua participação no total de viagens realizadas. Esta participação é obtida agrupando-se as viagens motorizadas em duas categorias: viagens motorizadas por modo coletivo e viagens motorizadas por modo individual. O percentual de cada um desses grupos no total de viagens motorizadas é a divisão modal. Analise o gráfico abaixo:

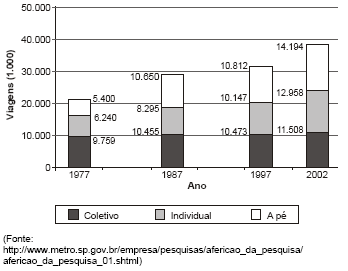
Com base no texto e na análise do gráfico, é correto afirmar:

• A.

  Em 2002, houve uma queda da divisão modal para o modo individual e parcela significativa das viagens deixou de ser realizada a pé.

• B.

  Em 1997, a divisão modal era de 53% para o modo coletivo e 47% para o modo individual. Em 2002, 37% das viagens eram realizadas a pé.

• C.

  Entre 1987 e 1997 houve um aumento na participação das viagens por modo coletivo, o que revela pela primeira vez a superação do modo individual pelo modo coletivo.

• D.

  Entre 1997 e 2002 houve diminuição da divisão modal para o modo coletivo, o que revela pela primeira vez a superação do modo coletivo pelo modo individual.

• E.

  A divisão modal para o modo coletivo continuou inalterada nas duas últimas décadas.

Para visualizar mais apropriadamente quanto as partes de uma população representam em relação ao todo, a partir de dados estatísticos, é mais adequado utilizar o

• A.

  histograma.

• B.

  gráfico por setores.

• C.

  diagrama de dispersão.

• D.

  polígono de freqüências.

• E.

  gráfico polar.

Considere o histograma abaixo que apresenta a distribuição dos salários dos empregados em uma empresa no mês de dezembro de 2007:

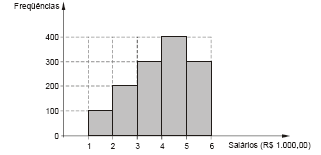
O valor da mediana dos salários dos empregados, considerando os intervalos de classe do histograma abertos à esquerda e fechados à direita e utilizando o método da interpolação linear, é igual a

• A.

  R$ 5.125,00

• B.

  R$ 4.125,00

• C.

  R$ 5.075,00

• D.

  R$ 4.750,00

• E.

  R$ 3.750,00

O histograma de freqüências absolutas abaixo apresenta a distribuição dos salários dos empregados de uma empresa no mês de dezembro de 2007. Dado: Considere que os intervalos de classe deste histograma são fechados à esquerda e abertos à direita.

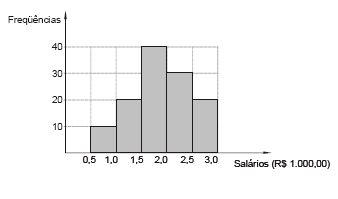
 Encontrou-se a média aritmética dos salários dos empregados, considerando que todos os valores incluídos em um certo intervalo de classe são coincidentes com o ponto médio deste intervalo. Obteve-se também a mediana dos salários utilizando o método da interpolação linear. O valor da moda dos salários (Mo) calculada conforme a fórmula Mo = 3Md − 2Me, sendo Md a mediana e Me a média aritmética, é igual a

• A.

  R$ 2.125,00

• B.

  R$ 1.950,00

• C.

  R$ 1.875,00

• D.

  R$ 1.750,00

• E.

  R$ 1.625,00

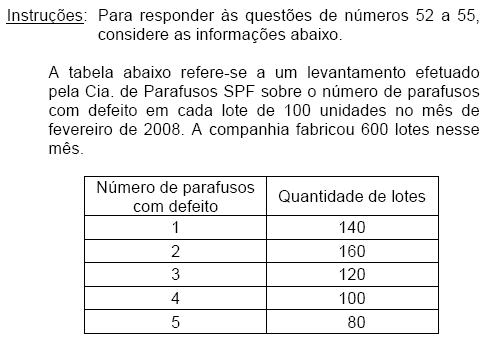
A mediana do número de parafusos com defeito dessa população é

• A.

  menor que a moda.

• B.

  maior que a média.

• C.

  menor que a média.

• D.

  maior que a média e a moda.

• E.

  menor que a média e a moda.

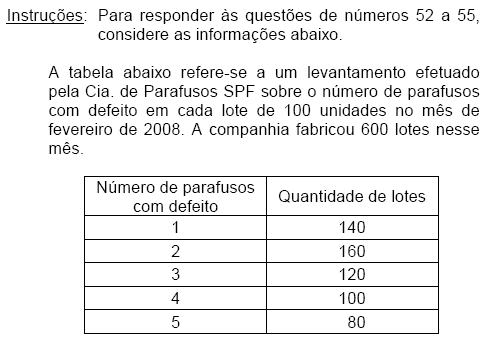
A moda do número de parafusos com defeito, dessa população, é

• A.

  menor que a mediana.

• B.

  igual à mediana.

• C.

  maior que a média.

• D.

  igual à média.

• E.

  maior que a mediana e inferior à média.

Um estudo realizado em uma população de tamanho infinito objetiva detectar a proporção de habitantes que possui determinado atributo. Uma amostra piloto adequada forneceu um valor de 25% para essa proporção. Deseja-se um intervalo de confiança de 95% para a estimativa dessa proporção, tendo o intervalo uma amplitude de 5%. Considerando a distribuição amostral da freqüência relativa dos habitantes possuidores do atributo normal e utilizando a informação da distribuição normal padrão (Z) que a probabilidade P(−2 ≤ Z ≤ 2) = 95%, temse que o tamanho da amostra deve ser de

• A.

  1.000

• B.

  1.200

• C.

  1.500

• D.

  1.800

• E.

  2.000

Das lâmpadas fabricadas por uma companhia extrai-se uma amostra de 100 lâmpadas e obtém-se a vida média de 1.000 horas. A vida das lâmpadas apresenta uma distribuição normal com um desvio padrão populacional igual a 100 horas. Considerando-se a população de tamanho infinito e a informação da distribuição normal padrão (Z), segundo a qual a probabilidade P(Z > 1,64) = 5%, obtémse um intervalo de confiança de 90% para a vida média das lâmpadas. A amplitude deste intervalo é igual a

• A.

  32,8 horas.

• B.

  36,0 horas.

• C.

  40,8 horas.

• D.

  60,0 horas.

• E.

  82,0 horas.

Sejam duas populações normalmente distribuídas de tamanho infinito e com a mesma variância σ² desconhecida. Deseja-se testar, ao nível de significância de 5%, que não há diferença entre as médias das duas populações. Para isso, utilizou-se uma amostra aleatória de 15 elementos da primeira população e de 12 da segunda, obtendo a seguir as respectivas médias amostrais. Em um teste t de Student, é correto afirmar:

• A.

  Há 5% de probabilidade do teste indicar uma diferença quando realmente ela não existe.

• B.

  O número de graus de liberdade, no caso, é igual a 26.

• C.

  O cálculo que leva à conclusão de rejeitar a hipótese nula, isto é, que as médias são iguais, independe do tamanho de cada amostra.

• D.

  Há 95% de probabilidade do teste mostrar que o procedimento é inadequado para testar a rejeição da hipótese nula.

• E.

  Há 95% de probabilidade do teste revelar que qualquer conclusão é incorreta.