Questões de Estatística da Núcleo de Computação Eletrônica UFRJ (NCE)

O gráfico a seguir refere-se às questões 24 e 25.

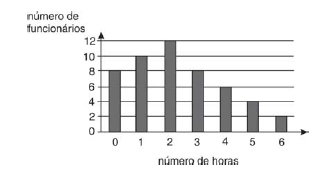
O número médio de horas semanais dedicadas a atividades físicas entre os funcionários pesquisados é:

• A. 2;
• B. 2,28;
• C. 2,5;
• D. 3;
• E. 3,28.

Em problemas de teste de hipóteses, o nível de significância de um teste pode ser definido como:

• A.

  a máxima probabilidade admitida de se rejeitar a hipótese nula, dado que a hipótese nula é verdadeira;

• B.

  a máxima probabilidade admitida de se rejeitar a hipótese nula, dado que a hipótese nula é falsa;

• C.

  a mínima probabilidade admitida de se rejeitar a hipótese alternativa, dado que a hipótese nula é verdadeira;

• D.

  a mínima probabilidade admitida de se rejeitar a hipótese nula, dado que a hipótese nula é verdadeira;

• E.

  a mínima probabilidade admitida de se rejeitar a hipótese nula, dado que a hipótese alternativa é verdadeira.

A tabela a seguir dá os valores de pares de observações (x_i, y_i ).

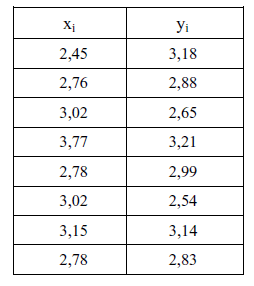
Para testar uma hipótese nula de que não há diferença entre as médias referentes à população X e à população Y, podemos usar o teste dos postos com sinal de Wilcoxon. O valor da estatística de teste para os dados apresentados pode ser:

• A.

  12

• B.

  14

• C.

  19

• D.

  24

• E.

  27

Deseja-se testar H₀: p = 1/2 contra H₁: p = 2/3, em que p é uma proporção populacional de "sucessos", com base numa amostra aleatória simples de tamanho 5 e com o critério que rejeita a hipótese nula de a proporção de "sucessos" na amostra for maior do que 70%. A probabilidade de se cometer erro tipo I com esse critério é:

• A.

  5/36;

• B.

  7/36;

• C.

  3/16;

• D.

  11/16;

• E.

  25/36.

Uma amostra aleatória simples de tamanho 100 será obtida de uma população normalmente distribuída com média μ desconhecida e variância 25. Para testar H0: μ ≥ 100 versus H1: μ < 100, o teste uniformemente mais poderoso de tamanho 0,05 rejeitará H0 se o valor da média amostral for:

• A.

  menor ou igual a 99,18;

• B.

  menor ou igual a 98,25;

• C.

  maior ou igual a 102,34;

• D.

  maior ou igual a 103,28;

• E.

  menor ou igual a 97,26.

Uma amostra aleatória simples X₁, X₂, ... , X_n de uma densidade uniforme no intervalo [ será observada. Uma estatística suficiente é:

• A.
• B.
• C.

  

• D.
• E.

A tabela a seguir informa a porcentagem de crianças de zero a cinco anos desnutridas por região, segundo pesquisa realizada em um determinado país.

Com base na tabela dada, a(s) afirmativa(s) cuja veracidade pode ser garantida é/são somente:

• A. I;
• B. II;
• C. III;
• D. I e II;
• E. I, II e III.

Num problema de estratificação amostral em L estágios, se W_h indica a proporção de elementos do estrato h na população, S_h representa a variância do estrato h e n é o tamanho da amostra então, na alocação ótima de Neyman, o tamanho da amostra em cada estrato será dado por:

• A.
• B.
• C.
• D.
• E.

Uma empresa de comércio varejista possui um cadastro de clientes, classificados por ordem alfabética, com informações acerca de uma série de variáveis. Ela planeja contatar, por telefone, uma amostra desses clientes para ouvi-los a respeito de uma certa promoção. Para fazer essa pesquisa, decide-se contatar o oitavo cliente do cadastro e, a seguir, o décimo oitavo, o vigésimo oitavo e assim por diante. O tipo de processo de amostragem usado nesse caso é o de amostragem:

• A.

  sistemática;

• B.

  aleatória simples;

• C.

  estratificada com sorteio aleatório;

• D.

  por conglomerados;

• E.

  estratificada em dois estágios.

Ainda em relação à análise de pares conjugados, sob a hipótese de que as 2n observações, realizadas em n indivíduos, provêm todas de uma mesma população contínua cuja densidade é simétrica, o valor esperado da estatística dos postos com sinal de Wilcoxon é:

• A. n(n - 1)/2;
• B. n(n + 1)/4;
• C. n(n – 1);
• D. n( n + 1)/2;
• E. n( n + 1)( n + 2 )/12.