Questões de Matemática

Ana Maria decidiu preparar uma torta cuja receita indicava 200 gramas de chocolate em barra. Em sua dispensa, havia uma barra de 350 gramas, mas ela não dispunha de uma balança para pesar a quantidade necessária. Então, ela decidiu dividir a barra em partes iguais e pegar a quantidade de partes que correspondessem a 200 gramas. Dentre os esquemas abaixo, em que os retângulos escuros correspondem às partes da barra de chocolate usadas por Ana Maria, aquele que representa os 200 gramas pedidos na receita é

• A.
• B.
• C.
• D.
• E.

André sobe uma escada de 48 degraus, mantendo uma velocidade constante de 2 degraus por segundo. No instante em que restam dois terços dos degraus para atingir o topo da escada, seu irmão, Renan, começa a subir a mesma escada com o intuito de alcançar André. A velocidade necessária para que Renan alcance André no instante em que este atinge o topo da escada é de:

• A.

  2,5 degraus por segundo.

• B.

  4 degraus por segundo.

• C.

  4,5 degraus por segundo.

• D.

  3 degraus por segundo.

• E.

  3,5 degraus por segundo.

Sendo x e y números reais tais que y = − 6x² +11x − 4 , o valor mínimo de x para o qual o valor correspondente de y é máximo é

• A.

  2/3.

• B.

  3/4.

• C.

  5/6.

• D.

  11/12.

• E.

  1.

Três números reais estão em progressão aritmética de razão 3 e dois termos dessa progressão são as raízes da equação x² - 2x - 8 = 0. Nesse caso, é correto afirmar que

a soma dos termos dessa progressão é superior a 4 e inferior a 8.

• C. Certo
• E. Errado

Considere que os termos da sequência (1, 2, 4, 5, 11, 12, 26, 27, 57, 58, . . .) foram obtidos segundo uma lei de formação. Segundo essa lei, o décimo quinto termo é um número

• A.

  maior que 500.

• B.

  divisível por 6.

• C.

  quadrado perfeito.

• D.

  múltiplo de 4.

• E.

  primo.

Na prateleira de um supermercado existem 170 garrafas de sucos de sabores diferentes: laranja, morango, tangerina e abacaxi. Sabe-se que:

• O número de garrafas de suco de morango corresponde a dois terços do número de garrafas de suco de abacaxi.

• O número de garrafas de suco de tangerina é igual a três quartos do número de garrafas de suco de laranja.

• O número de garrafas de suco de abacaxi é igual ao dobro do número de garrafas de suco de tangerina.

Marque a alternativa que indica a comparação correta entre o número de garrafas de cada sabor:

• A.

  morango > laranja > abacaxi > tangerina

• B.

  abacaxi > laranja > morango = tangerina

• C.

  laranja > tangerina > abacaxi > morango

• D.

  abacaxi > morango = laranja > tangerina

• E.

  laranja > abacaxi = morango > tangerina

Três números reais estão em progressão aritmética de razão 3 e dois termos dessa progressão são as raízes da equação x² - 2x - 8 = 0. Nesse caso, é correto afirmar que

o produto dos termos dessa progressão é um número real positivo.

• C. Certo
• E. Errado

Uma certa sacola de plástico suporta uma carga máxima de 15kg. O maior número de objetos de pesos iguais a 2/11 da carga máxima dessa sacola que podem ser transportados no interior da mesma é:

• A.

  3

• B.

  5

• C.

  8

• D.

  10

• E.

  6

Num jogo de arremessos em uma cesta de basquete, um grupo de amigos estabeleceu que para cada acerto, o jogador ganharia 3 pontos, e para cada erro perderia 2 pontos. Sabe-se que numa sequência de 20 arremessos por jogador, Fábio conseguiu um total de 15 pontos e Marcos, 10 pontos. O total de erros desses dois jogadores foi de:

• A.

  16

• B.

  18

• C.

  17

• D.

  19

• E.

  15

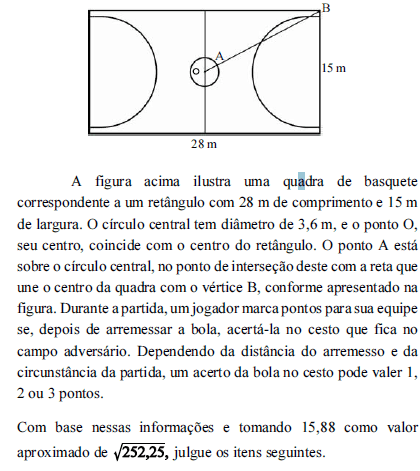
Se um time acertar a bola no cesto adversário 22 vezes, marcar um total de 42 pontos e o número de acertos de 2 pontos for o triplo do número de acertos de 3 pontos, então o número de acertos de 1 ponto será maior que 5.

• C. Certo
• E. Errado