Questões de Matemática

Texto para as questões 30 e 31

               Segundo Polya, se a educação não contribui para o desenvolvimento da inteligência, ela está obviamente incompleta. Desenvolver a habilidade de resolver problemas é essencial nesse processo e uma das principais metas do professor de matemática é fazer o máximo possível para que seus alunos desenvolvam a habilidade de resolver problemas.

                Várias situações do cotidiano podem ser utilizadas como situações-problema que podem ser apresentadas e resolvidas por alunos do ensino básico, como o exemplo a seguir.

                Um artesão comprava arame para fazer brincos a R$ 9,00 por metro. Cada par de brincos, feito com 20 cm de arame, era vendido a R$ 7,50. Recentemente, houve um aumento de R$ 1,50 no preço do metro de arame.

Ainda com relação à situação apresentada, considere que o lucro líquido do artesão obtido com venda de 10 pares de brincos, antes do aumento no preço do arame, era de R$ 25,00. Nesse caso, se todos os demais custos forem mantidos inalterados, para permanecer fixo o lucro líquido após o aumento no preço do arame, o artesão deve vender cada par de brincos por

• A.

  R$ 7,80.

• B.

  R$ 8,00.

• C.

  R$ 8,25.

• D.

  R$ 9,00.

No ponto x = 2, a função f assume um ponto de mínimo relativo que é também um ponto de mínimo absoluto.

• C. Certo
• E. Errado

Quanto falta a 0,32 para completar uma unidade?

• A. 0,78.
• B. 0,68.
• C. 0,46.
• D. 0,66.

Sérgio quer comprar 8 pacotes iguais  com kg de macarrão cada um. Ele deverá comprar

• A. 8 kg.
• B. 6 kg.
• C. 5 kg.
• D. 4 kg.

Em uma estação, os metrôs partem na direção leste de 30 em 30 minutos, e na direção sul, de 40 em 40 minutos. Em um instante, os metrôs partiram juntos, da mesma estação. Quanto tempo depois, isso acontecerá novamente, considerando ter sido mantida a regularidade?

• A. 100 minutos.
• B. 110 minutos.
• C. 120 minutos.
• D. 115 minutos.
• E. 90 minutos.

Texto para as questões de 58 a 60

Os conceitos e procedimentos relativos ao pensamento geométrico, inerentes aos alunos do 2.º segmento do EJA, relacionados ao raciocínio com proporções, incluem

• A.

  resolver situações-problema que envolvam figuras geométricas espaciais em procedimentos de ampliação e de redução.

• B.

  identificar, por exemplo, que as áreas de polígonos semelhantes variam na mesma proporção que os perímetros.

• C.

  identificar, por exemplo, que os volumes de sólidos semelhantes variam na mesma proporção que as áreas das superfícies desses sólidos.

• D.

  identificar, por exemplo, que ângulos são invariantes por transformações de semelhança.

O lucro de uma empresa, em milhares de reais, é dado pela função L(t) = f(t) – c(t), em que f(t) e c(t) representam, respectivamente, o faturamento e os custos da empresa, em milhares de reais, e t 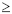 0 é o tempo, em meses, contado a partir do início do funcionamento da empresa. O gráfico de y = L(t), no sistema cartesiano yOt, é mostrado na figura a seguir.

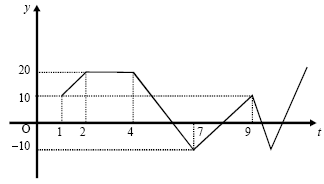
Com base nas informações acima, julgue os itens subseqüentes.

Se, para 4 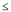t 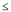7, os custos da empresa foram constantes e iguais a 40 mil reais — c(t) = 40 —, então o faturamento dessa empresa pode ser expresso por f(t) = -10t + 100.

• C. Certo
• E. Errado

Renato comprou um apartamento nas seguintes condições: deu de entrada R$ 60.000,00; deu quatro quotas de R$ 2.500,00 cada uma, e quinze prestações mensais de R$ 1.100,00 cada uma e sem acréscimo. Qual foi o preço desse imóvel?

• A. R$ 78.500,00.
• B. R$ 82.500,00.
• C. R$ 86.500,00.
• D. R$ 92.500,00.

Por dia, Marcelo dorme 8 horas e fica acordado 16 horas. A fração do dia que representa o número de horas que Marcelo dorme é

• A.
• B.
• C.
• D.

Tentativa e erro, padrões, simplificação, sentido inverso e simulação são algumas estratégias para resolução de problemas que podem ser ensinadas na escola. Na construção de retângulos, utilizando peças do tangram, a estratégia mais adequada é a de tentativa e erro. Esse procedimento está correto porque

• A.

  a partir da solução de casos particulares permite-se encontrar a solução geral.

• B.

  envolve pegar peças do tangram e verificar se é possível construir retângulos a partir delas.

• C.

  envolve desenhar um retângulo e tentar construí-lo utilizando peças do tangram.

• D.

  envolve a percepção da existência de um padrão comum nas peças do tangram que podem ser utilizadas para a construção de retângulos.