Questões de Matemática do ano 2006

A função lucro de uma empresa é dada por LT(q) = – 100q²+ 8000q + 2000. A quantidade que a empresa deve produzir para maximizar seu lucro é:

• A.

  40

• B.

  200

• C.

  800

• D.

  2000

• E.

  2040

A derivada da função f(x) = 1/x³ é:

• A.

  (x+1)⁻¹

• B.

  (x²)⁻¹

• C.

  −3/x²

• D.

  −3x−²

• E.

  −3x

A derivada da função f(x) = 1/x³ é:

• A.

  (x+¹)−¹

• B.

  (x²)−¹

• C.

  −3/x²

• D.

  −3x−²

• E.

  −3x

Uma piscina que tem capacidade para 27 m³ de água e está completamente cheia será esvaziada retirando-se 1,5 m³ de água a cada minuto. Nessa situação, considerando que f(t) seja o volume de água, em m³, que restará na piscina t min após o início da operação de esvaziamento, julgue os próximos itens.

No plano cartesiano xOy, o gráfico de y = f(t), com t em minutos e y em m³, é um segmento de reta que contém o ponto (10, 12).

• C. Certo
• E. Errado

Considere a equação y² - x² = 2x +1. Sabendose que as coordenadas inteiras desta equação são tais, que 2006 < x < y < 2100 , tem-se que o número de pares ordenados (x, y) , soluções desta equação, é:

• A. 90
• B. 91
• C. 92
• D. 93

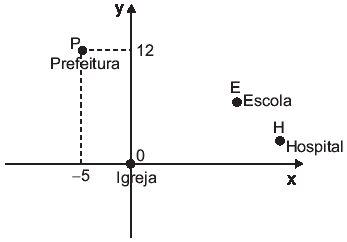
No centro de uma pequena cidade há uma igreja, uma escola, um hospital e a sede da prefeitura. Situando-se a igreja na origem de um plano cartesiano, a prefeitura fica no ponto P(−5; 12), como representado na figura abaixo.

Se cada unidade do gráfico corresponde a 100 m, a distância, em metros, entre a igreja e a prefeitura é de:

• A.

  500

• B.

  700

• C.

  1.200

• D.

  1.300

• E.

  1.700

O raio da circunferência de equação x² + y² 4x - 6y 1 = 0 vale:

• A. 12
• B. 2
• C. 1
• D.
• E.

Considere as circunferências A, B, C e D abaixo, representadas em um sistema de coordenadas cartesianas:

No quadro abaixo, estão apresentadas as equações das quatro circunferências anteriores:

Associando cada circunferência à sua equação obtemos:

• A.

  A-1, B-2, C-3 e D-4.

• B.

  A-4, B-3, C-2 e D-1.

• C.

  A-1, B-3, C-2 e D-4.

• D.

  A-4, B-2, C-3 e D-1.

• E.

  A-2, B-3, C-4 e D-1.

Às sete horas e vinte minutos, os ponteiros das horas e dos minutos de um relógio formam um ângulo que mede:

• A.

  90º;

• B.

  95º;

• C.

  100º;

• D.

  105º;

• E.

  110º.

Calcule o volume de um cilindro, com as seguintes dimensões: a base diâmetro é de 2,60 m e a altura é de 15,00m.

• A.

  245,04 m³.

• B.

  79,64 m³.

• C.

  122,52 m³.

• D.

  318,56 m³.