Questões de Matemática do ano 2008

No Brasil, é cada vez maior o número de pessoas que pesquisam preços na Internet. O responsável por um site de pesquisa de preços afirmou que, em 2002, o site recebia 2.000 acessos por dia enquanto que, em 2007, esse número subiu para 75.000. Se o aumento anual no número de acessos tivesse ocorrido de forma linear, formando uma progressão aritmética, qual teria sido, em 2006, o número de acessos diários a esse site?

• A.

  34.600

• B.

  45.700

• C.

  56.700

• D.

  60.400

• E.

  61.600

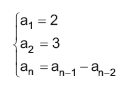
Qual é o 70^o termo da seqüência de números (a_n) definida acima?

• A.

  2

• B.

  1

• C.

  - 1

• D.

  - 2

• E.

  - 3

Um casal saiu em férias da cidade A até a cidade B e resolveu que iria fazer o percurso em 10 dias, parando todos os dias para descansar, estabelecendo o seguinte plano de viagem: no primeiro dia, viajaria 1024km, no segundo, 512km, no terceiro, 256km e assim sucessivamente.

Com base nesses dados, pode-se concluir que a distância entre as cidades A e B é superior a 2040km.

• C. Certo
• E. Errado

Um chefe entregou à sua secretária a tarefa de digitar um relatório de 200 páginas no prazo de 8 dias. No primeiro dia, a secretária digitou 10 páginas e, a partir daí, digitou, em cada dia, tantas páginas quantas havia digitado no dia anterior, mais 4.

Nessas condições, pode-se concluir que a secretária cumpriu com a tarefa no prazo estipulado.

• C. Certo
• E. Errado

• A.

  3.034

• B.

  3.255

• C.

  3.325

• D.

  3.470

• E.

  3.570

O problema apresentado a seguir, encontrado no Papiro Matemático Rhind ou Ahmos — 1650 a.C —, envolve a noção de progressão aritmética. "Divida 100 pães por 5 homens, de modo que as quantidades recebidas por cada um estejam em progressão aritmética e que a soma das duas quantidades menores seja igual a  da soma das outras três." Com base nessas informações e designando por a o termo inicial e por r a razão da progressão aritmética, julgue os itens a seguir.

Desconsiderando as hipóteses do problema egípcio, dividindo os 100 pães entre os 5 homens de forma que as quantidades recebidas por cada um estejam em uma progressão aritmética de razão 3, então o número máximo de pães que um dos homens receberia é igual a 29.

• C. Certo
• E. Errado

O problema apresentado a seguir, encontrado no Papiro Matemático Rhind ou Ahmos — 1650 a.C —, envolve a noção de progressão aritmética. "Divida 100 pães por 5 homens, de modo que as quantidades recebidas por cada um estejam em progressão aritmética e que a soma das duas quantidades menores seja igual a  da soma das outras três." Com base nessas informações e designando por a o termo inicial e por r a razão da progressão aritmética, julgue os itens a seguir.

Se b₁ = a, b₂ = a + r, b₃ = a + 2r, b₄ = a + 3r e b₅ = a + 4r são os cinco termos da progressão aritmética, então b₃ + b₄ + b₅ = 3 (b₃ + r).

• C. Certo
• E. Errado

A razão da progressão geométrica das idades é superior a 2/3 .

• C. Certo
• E. Errado

Os números a₃, a₅, e a₆ formam, nessa ordem, uma progressão aritmética.

• C. Certo
• E. Errado

O problema apresentado a seguir, encontrado no Papiro Matemático Rhind ou Ahmos - 1650 a.C -, envolve a noção de progressão aritmética.

"Divida 100 pães por 5 homens, de modo que as quantidades recebidas por cada um estejam em progressão aritmética e que a soma das duas quantidades menores seja igual a 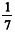da soma das outras três."

 Com base nessas informações e designando por a o termo inicial e por r a razão da progressão aritmética, julgue os itens a seguir.

Desconsiderando as hipóteses do problema egípcio, dividindo os 100 pães entre os 5 homens de forma que as quantidades recebidas por cada um estejam em uma progressão aritmética de razão 3, então o número máximo de pães que um dos homens receberia é igual a 29.

• C. Certo
• E. Errado