Questões de Matemática do ano 2008
Lista completa de Questões de Matemática do ano 2008 para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
No sistema de coordenadas cartesianas ortogonais xOy, a equação da reta tangente ao gráfico da função y = x 2 , que é paralela à reta que contém os pontos (0, 0) e (2, 4) é dada por
- A.
y = 2x - 1
- B.
y= 1/2 x - 1
- C.
y= -2x + 1
- D.
y= x - 2
- E.
y = 2/3 x + 2
Considere, em um sistema de coordenadas cartesianas ortogonais xOy, a região de área finita e limitada pelos gráficos das funções f(x) = x2 e g(x) = 9. Se a reta y = K divide essa região em duas partes de áreas iguais, então K é tal que
- A.
K3 = 27
- B.
K2/3 = 27/2
- C.
K3 = 9/2
- D.
K3/2 = 9/4
- E.
K3 = 27/16
Considere uma função f:D→ R , definida no domínio D=(−∞,0)∪(0,3)∪(3,+∞). Em seu domínio, a função f é contínua e tem derivadas contínuas até a ordem 2. As retas x = 0 e x = 3 são assíntotas verticais de f e a reta y = 1 é assíntota horizontal de f. O gráfico da f é apresentado na figura abaixo.
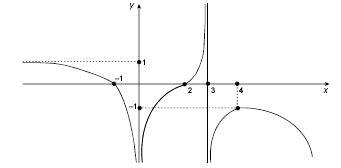
Com base no gráfico de f e nas informações acima, assinale a opção correta.
- A.

- B.
A função f não muda de concavidade.
- C.
Se x ∈ (0,3) então f (x)× f′(x)>0 .
- D.
A função f é injetiva.
- E.
Se x∈(3,+ ∞) então f ′(x)≠0 .
Com relação à função f (x) = x 3 + 2x 2 - 4x + 5, assinale a opção correta.
- A.
Em três pontos do gráfico da f, a reta tangente é horizontal.
- B.
A função f possui um máximo local no ponto

- C.
O gráfico da função f muda de concavidade nos pontos de abcissas x = -2 e

- D.

- E.
No intervalo (-2, -1), a função f é crescente.
Considerando a função y = f (x) = x2 – 5x + 6, em um sistema de coordenadas cartesianas ortogonais xOy, julgue os itens que se seguem.
Se g(x) = e x , então o gráfico da função h(x) = f (g(x)) intercepta o eixo Ox nos pontos de abcissas x1 = ln 2 e x2 = ln 3.
- C. Certo
- E. Errado
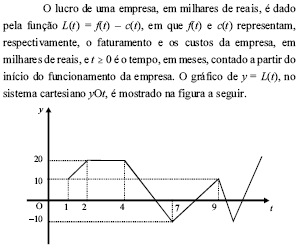
Com base nas informações acima, julgue os itens subseqüentes.
Suponha-se que, para 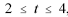 , o faturamento f(t) e os custos c(t) da empresa tenham sido constantes e diretamente proporcionais aos números 3 e 2, respectivamente. Nesse caso, é correto concluir que os custos dessa empresa foram inferiores a 35 mil reais.
, o faturamento f(t) e os custos c(t) da empresa tenham sido constantes e diretamente proporcionais aos números 3 e 2, respectivamente. Nesse caso, é correto concluir que os custos dessa empresa foram inferiores a 35 mil reais.
- C. Certo
- E. Errado
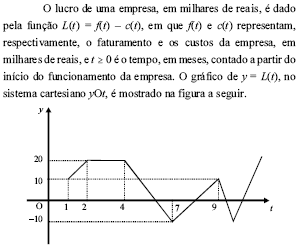
Com base nas informações acima, julgue os itens subseqüentes.
No período em que 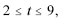 , o faturamento da empresa foi igual aos seus custos em apenas 2 momentos.
, o faturamento da empresa foi igual aos seus custos em apenas 2 momentos.
- C. Certo
- E. Errado
Julgue os itens subseqüentes.
A figura abaixo ilustra corretamente o gráfico, no plano cartesiano xOy, da função y = 2x-1.
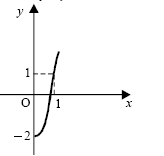
- C. Certo
- E. Errado
O lucro diário, em reais, de uma empresa obtido com a venda de uma unidade de determinado produto é dado por x – 5, em que x é o preço em reais de venda de uma unidade desse produto. A quantidade do referido produto vendida pela empresa em um dia é igual a 45 – x.
Com respeito a essa situação, julgue os itens a seguir.
O lucro total diário com esse produto vendendo-se a quantidade acima referida será igual a zero para x = 5 e x = 45.
- C. Certo
- E. Errado
Com relação a equações e funções de 1.º e 2.º graus e logaritmos, julgue os itens que se seguem.
No sistema de coordenadas cartesianas xOy, considere uma função de 2.º grau y = f (x) = Ax2 + Bx + C em que a reta x = -2 é o eixo de simetria do gráfico de f e x = -6 é uma raiz da equação polinomial f (x) = 0. Então, necessariamente, a equação polinomial f (x) = 0 tem mais uma raiz e essa raiz é um número maior que 1.
- C. Certo
- E. Errado


