Questões de Matemática do ano 2008

Considerando que a função 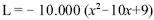 represente o lucro ou o prejuízo mensal, em reais, obtido por uma fábrica, na venda de x milhares de seu produto, julgue os itens a seguir.

O lucro mensal máximo que a fábrica poderá obter é superior a R$ 150.000,00.

• C. Certo
• E. Errado

Considerando que a função 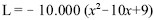 represente o lucro ou o prejuízo mensal, em reais, obtido por uma fábrica, na venda de x milhares de seu produto, julgue os itens a seguir.

A fábrica não obterá um lucro mensal no valor de R$ 180.000,00.

• C. Certo
• E. Errado

Considerando que a função 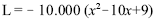 represente o lucro ou o prejuízo mensal, em reais, obtido por uma fábrica, na venda de x milhares de seu produto, julgue os itens a seguir.

Se o lucro mensal da fábrica for de R$ 120.000,00, então ela terá vendido menos de 2.500 unidades de seu produto.

• C. Certo
• E. Errado

Texto para as questões 55 e 56

De acordo com Butts, o problema proposto pelo professor trata-se apenas de um(a)

• A.

  exercício algorítmico.

• B.

  problema de aplicação.

• C.

  problema de pesquisa aberta.

• D.

  situação problema.

Texto para as questões 48 e 49

A construção correta de tabela, utilizando uma planilha eletrônica, consistindo de 5 colunas contendo, em cada coluna, os valores de x, f (x), g (x), (fºg)(x) e (gºf)(x) — fºg e gBf são, respectivamente, as composições de f com g e de g com f —, possibilitaria que os alunos inferirem que, para x > 2,

• A.

  fºg  gºf.

• B.

  g (x) × f (x) = 1.

• C.

  f é uma função par.

• D.

  f é a função inversa de g.

Texto para as questões 48 e 49

Considerando que os gráficos foram construídos corretamente, é correto afirmar que os gráficos de f e de g são simétricos em relação à reta

• A.

  x = 0.

• B.

  y = 0.

• C.

  y = x.

• D.

  y = -x.

Texto para as questões 46 e 47

Para resolver o item Q do problema, os alunos foram ao laboratório de informática e, com o auxílio de um software gráfico e de uma planilha, fizeram uma tabela e o gráfico da função R para x no intervalo [0, 200]. Essa atividade, possibilitou aos alunos observarem que

• A.

  a solução do problema corresponde ao vértice da parábola obtida ao traçar o gráfico da função R.

• B.

  o problema proposto tem sempre duas soluções distintas, independentemente do valor atribuído a R, exceto se R(x) = 10.500.

• C.

  a receita obtida na venda de 45 computadores é inferior àquela obtida na venda 55 computadores.

• D.

  para todo número natural x no intervalo considerando, tem-se que R(x)  0.

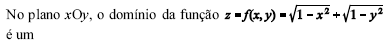
• A.

  quadrado de área 4.

• B.

  quadrado de área 1.

• C.

  círculo de raio 1.

• D.

  círculo de raio 2.

Considere o sólido obtido ao girar a região sob o gráfico da função y = x² , restrita ao intervalo [0, 1], e acima do eixo Ox, de 360º em torno do eixo Ox. Nesse caso, o volume desse sólido é igual a

• A.

  

• B.

  

• C.

  

• D.

Para a função y = x³ - 5x + 3 existem dois pontos do gráfico nos quais o ângulo que a reta tangente ao gráfico, nesses pontos, faz com o eixo Ox é igual a 45º. As abcissas desses pontos são, respectivamente,

• A.
• B.
• C.
• D.