Questões de Matemática do ano 2015

Em um clube formado por 35 amigos, 22 deles jogam basquete, 17 deles jogam vôlei e 8 deles jogam vôlei e basquete. Dessa forma assinale o item que contém a quantidade de amigos que não praticam nenhum dos dois esportes.

• A. 4
• B. 5
• C. 6
• D. 7

Numa determinada pesquisa feita por estudantes de uma escola, verificou-se que, das pessoas consultadas 100 liam a revista A, 150 liam a revista B, 20 liam das duas revistas e 110 não liam nenhuma revista. Quantas pessoas foram consultadas?

• A. 380
• B. 170
• C. 210
• D. 340

Observe a sequência a seguir e diga qual será o próximo número.

1 − 1 − 2 − 4 − 7 − 13 − 24 − ?

• A. 37
• B. 44
• C. 31
• D. 42

Jonas juntou 10% de seu salário durante 17 meses para dar de entrada em um automóvel, cujo preço é de R$ 34.000,00. Sabendo‐se que ele pagou 25% de entrada, então é correto afirmar que o salário de Jonas é igual a

• A. R$ 3.400,00.
• B. R$ 4.500,00.
• C. R$ 4.900,00.
• D. R$ 5.000,00.

Paulo comprou um terreno com as seguintes dimensões abaixo:

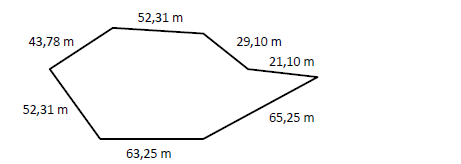
Para cercá‐lo, usou arame de R$ 2,50 o metro e cercou o terreno com três fiadas. O valor gasto por Paulo para cercar seu terreno foi de

• A. R$ 2.205,45.
• B. R$ 2.205,45.
• C. R$ 2.400,45.
• D. R$ 2.453,25.

Em um laticínio são vendidas caixas de leite em quatro recipientes diferentes conforme indicado na figura.

Se a diferença entre o volume de leite das caixas A e D é de quatro litros, então a soma dos valores da quantidade de leite que possui as quatro caixas é de

• A. 15.
• B. 14.
• C. 13.
• D. 12.

Em 2012, o mês de setembro começou em um sábado e terminou em um domingo. O próximo ano em que esse mesmo mês começará em um sábado e terminará em um domingo será

• A. 2015.
• B. 2016.
• C. 2017.
• D. 2018.

Um número inteiro “A” é composto por x algarismos. Considere que esse número pode ser escrito na forma do produto 5n², no qual n é igual ao número de vezes que o algarismo 5 aparece nos números inteiros entre 499 e 652. Sendo assim, a soma dos algarismos de “A” é

• A. 21.
• B. 23.
• C. 25.
• D. 27.

A figura representa um azulejo quadrado, cujo perímetro é igual a 64 cm e a superfície apresenta três pares de triângulos iguais. Considere que a área do triângulo A é quatro vezes maior que a área do triângulo B e que a área do triângulo B é quatro vezes maior que a área do triângulo C. Assim, a área da região em negrito, no interior desse azulejo, mede

• A. 148 cm2.
• B. 156 cm2.
• C. 172 cm2.
• D. 192 cm2.

Nota-se que é possível colocar todos os algarismos 1, 2, 3, 4, 5, 6, 7, 8 e 9, sem repeti-los, nas casas de um quadrado (3×3) para formar um quadrado mágico, ou seja, um quadrado onde a soma dos números nas linhas, nas colunas e diagonais, seja a mesma. Para que isto ocorra, necessariamente o número da casa central é:

• A. 3
• B. 4
• C. 5
• D. 6
• E. 7