Questões de Matemática do ano 2016

Se 3 é raiz do polinômio P(x) ≡ kx³ – 3x² – 7x – 3k, com K ∈ N, então:

• A. 9 < k.
• B. k < 2.
• C. 2 ≤ k < 5.
• D. 5 ≤ k < 9.

Sobre propriedades de logaritmos, marque V para as verdadeiras e F para as falsas.

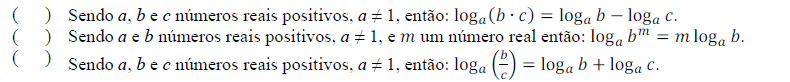
Assinale a sequência correta.

• A. F, F, V
• B. F, V, F
• C. V, V, F
• D. V, F, V

A função inversa de f (x) = 2^x + 1, com x ∈ R, é:

• A. y = log₂(x), com x > 0.
• B. y = log_1/2 (–x), com x < 0.
• C. y = log₂(x – 1), com x > 1.
• D. y = log₂(x + 1), com x < 1.

O valor da expressão log₂ 16 + log₄ 8 + log₈ 4 é igual a

• A. 5.
• B. 23/2.
• C. 37/6.
• D. 5/4.
• E. 41/8.

Seja a função quadrática g (x) = −x² + 5x + 24, definida com domínio R e contra-domínio R. A quantidade de números naturais do domínio que apresentam imagens positiva nessa função é igual a

• A. 12.
• B. 11.
• C. 7.
• D. 9.
• E. 8.

O gráfico abaixo é de uma função definida no intervalo real de −7 a 7.

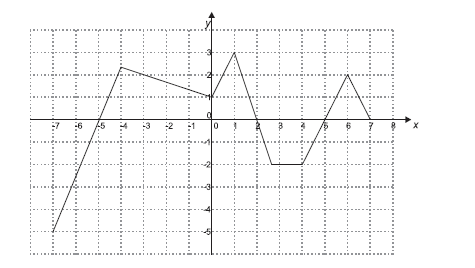
A soma dos zeros dessa função é igual a

• A. 14.
• B. 9.
• C. -3.
• D. 19.
• E. 0.

O gráfico de uma função polinomial do 1o grau crescente é uma reta de inclinação 45° que intersecta o eixo das ordenadas em y = −2. A equação geral dessa reta é

• A. x + y + 2 = 0.
• B. x + y − 2 = 0.
• C. x − y − 2 = 0.
• D. x − y + 2 = 0.
• E. 2x + y + 2 = 0.

O triângulo I tem base b e altura h. O triângulo II tem base 25% maior e altura 20% menor que o triângulo I. A base do triângulo III é 1,25b e a altura é 0,8h. Pode-se afirmar que:

• A. a área do triângulo I é maior que a área do triângulo II.
• B. a área do triângulo II é menor que a área do triângulo III.
• C. os triângulos II e III têm a mesma área que é maior que a área do triângulo I.
• D. os triângulos II e III têm a mesma área que é menor que a área de triângulo I.
• E. os três triângulos têm a mesma área.

Ao duplicar a largura de um determinado retângulo e reduzir à metade o comprimento desse mesmo retângulo, obtém-se um quadrado de perímetro P.

O perímetro do retângulo original é

• A. 2,5P
• B. 0,25 P
• C. 1,25P
• D. 0,75P
• E. P

Considere as seguintes definições:

1 - Um triângulo é chamado de escaleno quando os seus lados possuem comprimentos diferentes.

2 - Um triângulo é chamado de isósceles quando há dois de seus lados com o mesmo comprimento.

3 - Um triângulo é chamado de equilátero quando todos os seus lados possuem o mesmo comprimento.

De acordo com as definições apresentadas, um triângulo não é escaleno quando, e apenas quando, ele

• A. é isósceles.
• B. é isósceles, mas não é equilátero.
• C. não é isósceles.
• D. não é equilátero, nem é isósceles.
• E. não é equilátero.