Questões sobre Trigonometria

Na figura, o triângulo ABC é eqüilátero (lados de mesma medida e ângulos de mesma medida). A soma das medidas, em graus, dos ângulos α e β é igual a

• A. 120°.
• B. 115°.
• C. 110°.
• D. 90°.
• E. 85°.

       A figura acima representa o setor a ser policiado por um grupo de agentes de segurança de uma certa cidade, envolvendo principais avenidas — linhas cheias — e ruas menores — linhas pontilhadas. Em cada um dos pontos marcados por letras maiúsculas existe um posto policial de apoio para essa equipe. As rondas são feitas em viaturas que possuem o mesmo rendimento, isto é, o mesmo consumo de combustível por hora de ronda. Considere que três viaturas com agentes de segurança consumam no total 27 litros de gasolina por um período de 6 horas de ronda. Considere, também, que os triângulos CID e DEF são semelhantes, com ângulos iguais nos vértices C e F, e que a medida do segmento CI é igual a 16,25 km. As dimensões de algumas ruas e avenidas representadas na figura são mostradas na tabela ao lado dessa figura.

Considerando as informações acima e sabendo que cada viatura percorre toda a região da ronda, julgue os itens subseqüentes.

A área do triângulo DEF é inferior a 21 km²

• C. Certo
• E. Errado

       A figura acima representa o setor a ser policiado por um grupo de agentes de segurança de uma certa cidade, envolvendo principais avenidas — linhas cheias — e ruas menores — linhas pontilhadas. Em cada um dos pontos marcados por letras maiúsculas existe um posto policial de apoio para essa equipe. As rondas são feitas em viaturas que possuem o mesmo rendimento, isto é, o mesmo consumo de combustível por hora de ronda. Considere que três viaturas com agentes de segurança consumam no total 27 litros de gasolina por um período de 6 horas de ronda. Considere, também, que os triângulos CID e DEF são semelhantes, com ângulos iguais nos vértices C e F, e que a medida do segmento CI é igual a 16,25 km. As dimensões de algumas ruas e avenidas representadas na figura são mostradas na tabela ao lado dessa figura.

Considerando as informações acima e sabendo que cada viatura percorre toda a região da ronda, julgue os itens subseqüentes.

A razão de semelhança do triângulo CID para o triângulo DEF é igual a 1,625.

• C. Certo
• E. Errado

       A figura acima representa o setor a ser policiado por um grupo de agentes de segurança de uma certa cidade, envolvendo principais avenidas — linhas cheias — e ruas menores — linhas pontilhadas. Em cada um dos pontos marcados por letras maiúsculas existe um posto policial de apoio para essa equipe. As rondas são feitas em viaturas que possuem o mesmo rendimento, isto é, o mesmo consumo de combustível por hora de ronda. Considere que três viaturas com agentes de segurança consumam no total 27 litros de gasolina por um período de 6 horas de ronda. Considere, também, que os triângulos CID e DEF são semelhantes, com ângulos iguais nos vértices C e F, e que a medida do segmento CI é igual a 16,25 km. As dimensões de algumas ruas e avenidas representadas na figura são mostradas na tabela ao lado dessa figura.

Considerando as informações acima e sabendo que cada viatura percorre toda a região da ronda, julgue os itens subseqüentes.

Os triângulos ABC e HIG são semelhantes.

• C. Certo
• E. Errado

       A figura acima representa o setor a ser policiado por um grupo de agentes de segurança de uma certa cidade, envolvendo principais avenidas — linhas cheias — e ruas menores — linhas pontilhadas. Em cada um dos pontos marcados por letras maiúsculas existe um posto policial de apoio para essa equipe. As rondas são feitas em viaturas que possuem o mesmo rendimento, isto é, o mesmo consumo de combustível por hora de ronda. Considere que três viaturas com agentes de segurança consumam no total 27 litros de gasolina por um período de 6 horas de ronda. Considere, também, que os triângulos CID e DEF são semelhantes, com ângulos iguais nos vértices C e F, e que a medida do segmento CI é igual a 16,25 km. As dimensões de algumas ruas e avenidas representadas na figura são mostradas na tabela ao lado dessa figura.

Considerando as informações acima e sabendo que cada viatura percorre toda a região da ronda, julgue os itens subseqüentes.

O triângulo ABC é isósceles.

• C. Certo
• E. Errado

Em cada um dos itens de 25 a 28, é apresentada uma situação hipotética, seguida de uma assertiva a ser julgada.

O piso de uma sala deve ser revestido com peças de
cerâmica em forma de triângulos retângulos isósceles cuja
hipotenusa mede 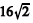 cm. Calculou-se que seriam
necessárias pelo menos 3.000 peças para cobrir todo o piso.
Nessa situação, conclui-se que a área desse piso é superior
a 38 m².

• C. Certo
• E. Errado

Um avião levanta vôo formando um ângulo de 12º com o chão. Mantendo essa inclinação, a que distância do ponto de partida ele vai estar quando atingir 3 km de altura? (Dados sen 12º = 0,208, cos 12º = 0,978 e tg 12º = 0,213)

• A. 3,067 km
• B. 14,423 km
• C. 14,085 km
• D. 2,934 km
• E. 14,555 km

Julgue o item que se segue, acerca de funções e equações trigonométricas e de geometria plana.

Considere que A e B sejam pontos localizados em margens opostas de um rio; escolhendo-se um ponto C, a 100 m de A, na mesma margem do rio, mediram-se os ângulos do triângulo ABC e determinou-se que o ângulo no vértice A era igual a 60º, e no vértice C, 45º. Nessa situação, a distância entre os pontos A e B é inferior a 80 m.

• C. Certo
• E. Errado

Na figura acima, está esquematizado o projeto de construção de um oleoduto que deverá ligar uma plataforma de prospecção de petróleo, localizada em alto mar, a uma refinaria da PETROBRAS, localizada em terra firme. O ponto indicado por A na figura é o local em terra firme mais próximo da plataforma, e a distância de A à plataforma é igual a D km. A refinaria está localizada no ponto B, à distância de d km do ponto A. O segmento AB, todo em terra firme, é perpendicular ao segmento que liga a plataforma ao ponto A. Sabe-se que o custo por quilômetro de oleoduto construído no mar é igual a P reais e, em terra firme,  a reais. Assim, deseja-se determinar um ponto C, em terra firme e sobre o segmento AB, de forma que, construindo-se o oleoduto no mar, da plataforma ao ponto C, e, em terra firme, de C à refinaria, o custo total do oleoduto a ser construído seja o menor possível.

Com base nessas informações e considerando que x é a distância de A a C e y é a distância de C a B, em km, julgue os itens que se seguem.

A função f que descreve o custo total de construção do oleoduto, em relação a x e a y, pode ser corretamente expressa por: f(x,y)=

• C. Certo
• E. Errado

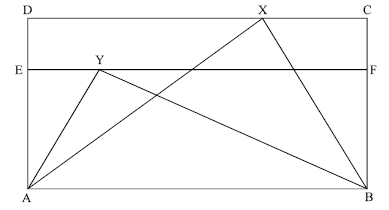
Na figura acima, ABCD e EFCD são dois retângulos e ABX e ABY são triângulos de bases AB e vértices sobre os segmentos DC e EF, respectivamente. O segmento EF é paralelo à base AB do retângulo ABCD. Sabe-se que a área do retângulo EFCD é igual a 30% da área do retângulo ABCD. Considerando essas informações, julgue os itens que se seguem.

A área do triângulo ABY é igual a 70% da área do triângulo ABX.

• C. Certo
• E. Errado