Questões de Matemática da Fundação CESGRANRIO (CESGRANRIO)

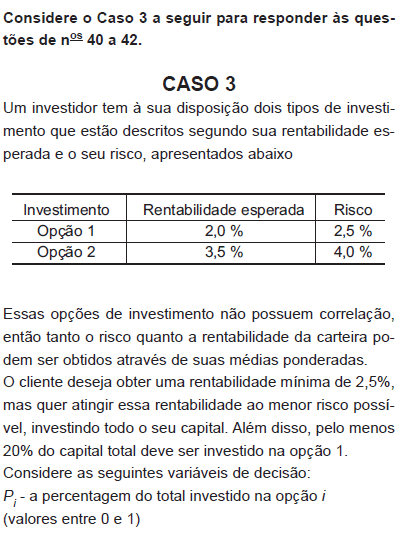Qual a função-objetivo que pode ser utilizada na modelagem do caso, de maneira a minimizar o risco da carteira?

• A. Min 0,025P₁ + 0,04P₂
• B. Min 0,02P₁ + 0,035P₂
• C.
• D.
• E. Min P₁ + P₂

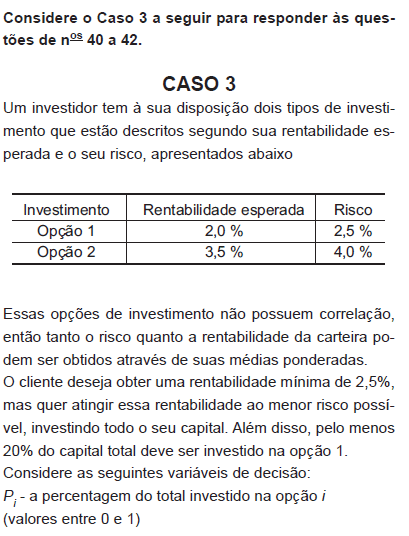A inequação que representa a restrição rentabilidade mínima é dada por

• A. P₁ + P₂ > 0,025
• B. 0,025P₁ + 0,04P₂ > 0,025
• C.
• D. 0,02P₁ + 0,035P₂ > 0,025
• E. 0,02P₁ + 0,035P₂ > 0,025

A restrição que representa a condição de que todo o capital do cliente será investido é

• A. 1
• B. P₁ + P₂ <1
• C. P₁ + P₂ <100
• D. P₁ + P₂ = 1
• E. P₁ + P₂ = 100

A Regra do Fluxo Balanceado, nesse caso, é dada pela seguinte expressão para cada Nó da rede:

• A. Saídas_{nó i} - Entradas_{nó i} < Oferta_{nó i} ou Demanda_{nó i}
• B. Saídas_{nó i} - Entradas_{nó i} > Oferta_{nó i} ou Demanda_{nó i}
• C. Entradas_{nó i} - Saídas_{nó i} = Oferta_{nó i} ou Demanda_{nó i}
• D. Entradas_{nó i} - Saídas_{nó i} < Oferta_{nó i} ou Demanda_{nó i}
• E. Entradas_{nó i} - Saídas_{nó i} > Oferta_{nó i} ou Demanda_{nó i}

• A.
• B.
• C.
• D.
• E.

Para comprar um carro novo, foram identificados 4 modelos das indústrias A, B, C e D. A decisão será tomada de acordo com preço e consumo de combustível. É evidente que a preferência é por um carro mais barato que consuma menos combustível. Nesse caso, tem-se um problema com 4 alternativas e 2 critérios. As características dos 4 modelos são apresentadas através dos pares de coordenadas A=(36,8), B=(35,7), C=(34,8) e D=(35,9), onde a primeira coordenada refere-se ao preço (dado em R$ 1.000,00) e a segunda refere-se ao consumo de combustível (dado em litro por quilômetro). Em relação ao conjunto viável, conclui-se que

• A. A e D são pontos não dominados.
• B. B e C são pontos eficientes.
• C. B e D são pontos eficientes.
• D. C e D são soluções não dominadas.
• E. B e C são soluções dominadas.

Um fabricante de leite estabelece a seguinte promoção: 3 caixas vazias do leite podem ser trocadas por uma caixa cheia desse mesmo produto. Cada caixa contém 1 litro. Comprando-se 11 caixas desse leite, a quantidade máxima, em litros, que pode ser consumida é

• A.

  13

• B.

  14

• C.

  15

• D.

  16

• E.

  17

Em Teoria dos Jogos, uma das clássicas hipóteses é de que os jogadores tomem decisões

• A. com base em conjuntos distintos de estratégias.
• B. com base em experiências de sucesso passadas.
• C. com base nas possibilidades de ganhos ou perdas de alguns de seus oponentes.
• D. em acordo com um subconjunto de participantes, visando a maximizar perdas dos demais.
• E. puramente racionais.

No caso de duas concorrentes (ABC e XYZ) que apresentam esse quadro de estratégias no contexto da Teoria dos Jogos, verifica-se que, para a empresa ABC,

• A. a estratégia RJ domina a estratégia SP.
• B. a estratégia RJ domina a estratégia MG.
• C. a estratégia SP domina a estratégia MG.
• D. a estratégia MG domina a estratégia SP.
• E. não existe estratégia dominante.

Existe uma regra prática de divisibilidade por 7 com o seguinte procedimento:

Separa-se o último algarismo da direita. Multiplica-se esse algarismo por 2 e tal resultado é subtraído do número que restou sem o algarismo à direita. Procede-se assim, sucessivamente, até se ficar com um número múltiplo de 7, mesmo que seja zero.

Veja os exemplos a seguir:

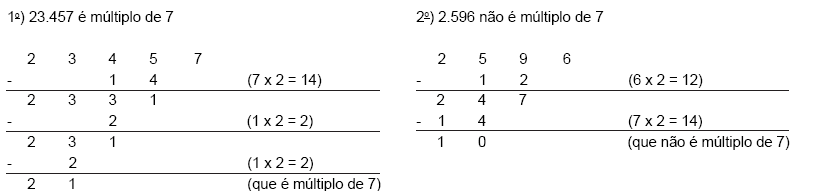
 Seja a um algarismo no número a13.477.307. O valor de a para que este número seja divisível por 7 é

• A.

  1

• B.

  3

• C.

  5

• D.

  7

• E.

  9