Questões de Matemática da Fundação CESGRANRIO (CESGRANRIO)

No caso das duas concorrentes (ABC e XYZ), adotandose o método de eliminação sequencial de estratégias dominadas, básico no contexto da Teoria dos Jogos, concluise que a empresa ABC

• A. ganhará 40% do mercado.
• B. ganhará 20% do mercado.
• C. ganhará 10% do mercado.
• D. continuará com a mesma fatia de mercado.
• E. perderá 10% do mercado.

Um homem entra numa livraria, compra um livro que custa 20 reais e paga com uma nota de 100 reais. Sem troco, o livreiro vai até a banca de jornais e troca a nota de 100 por 10 notas de 10 reais. O comprador leva o livro e 8 notas de 10 reais. Em seguida, entra o jornaleiro dizendo que a nota de 100 reais é falsa. O livreiro troca a nota falsa por outra de 100, verdadeira. O prejuízo do livreiro, em reais, sem contar o valor do livro, foi

• A.

  200

• B.

  180

• C.

  100

• D.

  80

• E.

  20

Uma rede de seis localidades é composta por dois fornecedores de determinado produto (localidades 1 e 2), dois centros consumidores desse produto (localidades 3 e 4) e duas localidades (5 e 6), onde ocorre apenas transbordo, isto é, passagem do produto, sem retenção. Considere a seguinte notação: Qij = quantidade de produto fluindo da localidade i para a localidade j; Cij = custo de transportar cada unidade desse produto de i para j; Tij = quantidade máxima transportável da localidade i para a j; Pi = quantidade de produto disponível no fornecedor i (se positiva) ou demandada pelo consumidor i (se negativa). No caso das localidades 5 e 6 onde ocorre apenas o transbordo, tem-se Pi = 0. Se o objetivo for determinar o menor custo possível para o fluxo do produto na rede dos fornecedores 1 e 2 para os consumidores 3 e 4, eventualmente passando pelas localidades 5 e 6, devem ser observadas as seguintes restrições para todo i e todo j:

• A.
• B.
• C.
• D.
• E.

Considerando-se N um número inteiro e positivo, analise as afirmações seguintes, qualquer que seja o valor de N:

I - N² + N + 1 é um número ímpar;

II - N⋅ (N + 1) ⋅ (N + 2) é um número múltiplo de 3;

III - N² tem uma quantidade par de divisores;

IV - N + (N + 1) + (N + 2) é um número múltiplo de 6.

 A quantidade de afirmações verdadeiras é

• A.

  1

• B.

  2

• C.

  3

• D.

  4

• E.

  0

Um quadrado é cortado em 17 quadrados menores. Todos esses quadrados têm as medidas de seus lados, em centímetros, expressas por números inteiros positivos. Há exatamente 16 quadrados com área igual a 1 cm². A área do quadrado original, em cm², vale

• A.

  81

• B.

  64

• C.

  49

• D.

  36

• E.

  25

O tempo entre as ocorrências de emergências e o tempo consumido para resolvê-las pelo especialista são usualmente modelados por Distribuições Exponenciais. Se, em média, o tempo entre ocorrências é de 6h e, em média, o tempo necessário para o especialista solucioná-las é de 3h, então

• A. 0.
• B. a probabilidade de o especialista demorar mais que 3h em um atendimento é e⁻¹.
• C. a probabilidade de o intervalo entre duas ocorrências ser superior a 2h é dada por e⁻².
• D. a probabilidade de o intervalo entre duas ocorrências ser inferior a 2h é dada por e⁻².
• E. a probabilidade de o intervalo entre duas ocorrências ser superior a 2h é dada por 2e⁻².

No âmbito da programação linear, minimizar

• A.

  minimizar z’ = (2001.x₁+2010.x10)/₂ , com z’=z

• B.

  minimizar z’ = -2001.x₁+2002.x₂-2003.x₃+...+2010.x10 , com z’=-z

• C.

  maximizar z’ = -2001.x₁-2002.x₂-2003.x₃-...-2010.x₁₀ , com z’=-z

• D.

  maximizar z’ = (2001.x₁+2010.x₁₀)/2 , com z’=z

• E.

  maximizar z’ = +2001.x₁-2002.x₂+2003.x₃-...-2010.x₁₀ , com z’=2.z

O valor máximo da função de variável real 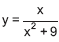 é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

O gráfico abaixo mostra a curva de custo total médio de uma empresa, em função da quantidade produzida.

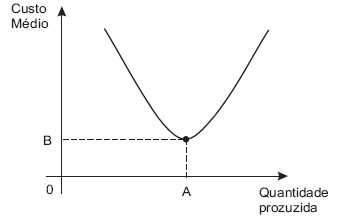
Considerando o gráfico, afirma-se que o(a)

• A.

  custo variável de produção é nulo.

• B.

  custo fixo de produção é necessariamente nulo.

• C. custo total diminui com o aumento da produção até A.
• D.

  empresa deve produzir a quantidade A para maximizar seu lucro.

• E.

  curva de custo marginal passa pelo ponto de coordenadas (A, B).

• A.
• B.
• C.
• D.
• E.