Questões de Matemática da Escola de Administração Fazendária (ESAF)

A fração etiológica ou fração atribuível de acidente vascular cerebral entre mulheres do grupo "fumantes" e aquelas do grupo "nunca fumou" é de (valores aproximados):

• A. 150%
• B. 60 %
• C. 34 %
• D. 40%
• E. 66,67%

O risco absoluto ou excesso de risco de acidente vascular cerebral entre mulheres do grupo "fumantes" e aquelas do grupo "nunca fumou" é de (valores aproximados):

• A. 30 por 100.000 pessoas-ano
• B. 60 %
• C. 34 %
• D. 27 por 100.000 pessoas-ano
• E. 7 por 100.000 pessoas-ano

Obtenha a função derivada de f(x) = e^−2x (3x² − 2).

• A.

  −2e^−2x (3x² −3x).

• B.

  2e^−2x (3^x2 −3x).

• C.

  6xe^−2x

• D.

  −2e^−2x (3x² − 2).

• E.

  −2e^−2x (3^x2 −3x − 2).

Em um triângulo ABC qualquer, um dos lados mede 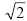 cm e um outro mede 2 cm. Se o ângulo formado por esses dois lados mede 45°, então a área do triângulo é igual a

• A. 3^-1/3
• B. 2^1/2
• C. 2^-1/2
• D.
• E. 1

Os valores da função exponencial 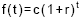, t real , c>0 e 1+r>0, nos pontos em que t é um número natural, constituem uma progressão geométrica. Indique a razão desta progressão.

• a.

  c.

• b.

  1+r.

• c.

  c-1.

• d.

  r.

• e.

  c(1+r).

O sistema dado pelas equações possui duas raízes, x e y.

Sabendo-se que "a" é uma constante, então a soma dos quadrados das raízes é igual a

• A. 1
• B. 2
• C. 4
• D. sen ð
• E. cos ð

Considere duas matrizes de segunda ordem, A e B, sendo que B = 2 ^1/4 A. Sabendo que o determinante de A é igual a 2^-1/2, então o determinante da matriz B é igual a:

• A. 2 ^1/2
• B. 2
• C. 2 ^-1/4
• D. 2 ^-1/2
• E. 1

Considere um terreno quadrado com o comprimento do lado medindo uma unidade. Indique qual o número racional p/q que representa a medida do comprimento da diagonal desse terreno.

• A. Tal número racional não existe porque essa medida é um número irracional
• B. p=1414, q=1000
• C. p=1414-14=1400, q=990
• D. p=141-14=127, q=90
• E. p=1414-141=1273, q=900

Considere duas matrizes quadradas de terceira ordem, A e B. A primeira, a segunda e a terceira colunas da matriz B são iguais, respectivamente, à terceira, à segunda e à primeira colunas da matriz A. Sabendo-se que o determinante de A é igual a x³, então o produto entre os determinantes das matrizes A e B é igual a:

• A. –x^-6
• B. –x⁶
• C. x³
• D. –1
• E. 1

O menor complementar de um elemento genérico xij de uma matriz X é o determinante que se obtém suprimindo a linha e a coluna em que esse elemento se localiza. Uma matriz Y = y^_ij, de terceira ordem, é a matriz resultante da soma das matrizes A = (a_ij) e B = (b_ij). Sabendo-se que (a_ij ) = (i+j)² e que b_ij = i² , então o menor complementar do elemento y₂₃ é igual a:

• A. 0
• B. -8
• C. -80
• D. 8
• E. 80