Questões de Matemática da Fundação Carlos Chagas (FCC)

Um ajudante de manutenção perguntou a seu supervisor quantas valas haviam sido abertas no dia anterior. O supervisor respondeu que, subtraindo-se 64 unidades do triplo do quíntuplo do número de valas abertas, obtém-se a terça parte do número de valas abertas, acrescida de 24 unidades. Supondo que o ajudante tenha resolvido corretamente o problema proposto pelo seu supervisor, então, a solução por ele encontrada era um número compreendido entre

• A.

  0 e 5

• B.

  5 e 10

• C.

  10 e 15

• D.

  15 e 20

• E.

  20 e 25

Sabendo-se que densidade é a razão entre a massa e o volume, um professor de matemática pediu que seus alunos calculassem a densidade de uma cola de bastão cilíndrico. Para o cálculo, os alunos obtiveram as seguintes informações e medidas do bastão:

− raio da base do cilindro de cola mede 2 cm
− a altura do cilindro de cola mede 6 cm
− a embalagem indica haver 31 g de cola no cilindro

Adotando π = 3,1 e com base nos dados coletados, a densidade da cola, em g/cm³, é de, aproximadamente,

• A.

  0,34

• B.

  0,38

• C.

  0,42

• D.

  0,46

• E.

  0,50

Sabendo que o trabalho com contra-exemplos pode favorecer a compreensão de muitas idéias matemáticas, um professor pediu que os alunos buscassem um contra-exemplo para mostrar que cada uma das implicações abaixo é falsa.

• A.

  0,6

• B.

  0,4

• C.

  −0,3

• D.

  −0,4

• E.

  −0,6

As distâncias Terra-Lua e Terra-Andrômeda são de, aproximadamente, 4 . 10⁸ m e 2 . 10²² m, respectivamente. Se representássemos em uma reta a distância Terra-Lua por 1 mm, nessa mesma reta a distância Terra-Andrômeda seria representada por

• A.

  500 km.

• B.

  5 mil km.

• C.

  500 mil km.

• D.

  5 milhões de km.

• E.

  50 milhões de km.

Dada uma fração irredutível, sabemos que sua representação decimal necessariamente é uma dízima periódica se e somente se

• A.

  o denominador é um número primo.

• B.

  o denominador é um número ímpar.

• C.

  a fatoração do numerador apresenta apenas fatores pares.

• D.

  a fatoração do denominador apresenta fatores diferentes de 2 e 5.

• E.

  a fatoração do denominador não apresenta fatores ímpares.

Observe a folha que a professora de Matemática distribuiu a cada um de seus alunos da 8ª A e o que ela disse em seguida.

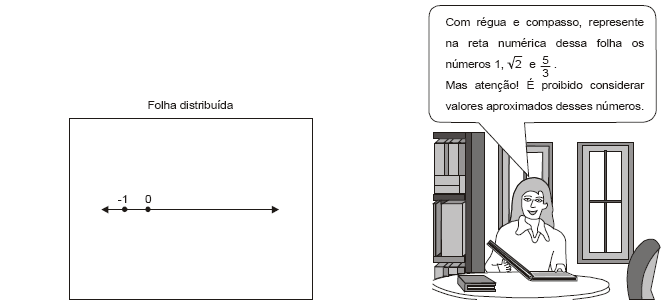
Com essa pequena atividade, a professora mostra que considera "Construções Geométricas" como uma ferramenta

• A.

  que permite integrar conhecimentos de geometria e de números.

• B.

  que deve ser trabalhada de modo independente de grandezas e medidas.

• C.

  adequada para desenvolver o ensino de probabilidades.

• D.

  indispensável no desenvolvimento do ensino e aprendizagem das unidades de medida de massa e volume e suas relações.

• E.

  que deve ser trabalhada pelo professor de Educação Artística, em Desenho Geométrico.

O gráfico abaixo indica uma pesquisa feita com os alunos de uma classe sobre a mão que utilizam para escrever.

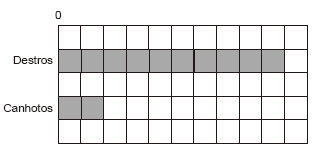
Sabe-se que todos os 47 alunos da sala responderam a pesquisa e que apenas um deles assinalou duas respostas, por ser ambidestro. Assim, é correto afirmar que cada quadrado da malha representa um total de respostas igual a

• A.

  2

• B.

  3

• C.

  4

• D.

  6

• E.

  8

Um professor propôs a seus alunos de 5a série o seguinte problema:

Paulo e Luana, professores das 5as séries de uma escola resolveram elaborar as questões de uma prova para todas essas séries, de modo que Paulo se incumbiu das questões de número ímpar e Luana as de número par, em igual quantidade. Assim, pode-se concluir que o número que identificou a última questão dessa prova é, com certeza,

I. múltiplo de 3.
II. um número primo diferente de 2.
III. um número par.
IV. um número fracionário.

Com tal problema, é possível que esse professor tenha tido a intenção de levar seus alunos a

• A.

  identificar os múltiplos de 3, observando regularidades na seqüência de tais múltiplos.

• B.

  trabalhar com potências de números naturais com expoentes inteiros.

• C.

  reconhecer e relacionar propriedades dos números fracionários.

• D.

  estabelecer relações quantitativas entre subconjuntos do conjunto dos números naturais.

• E.

  decompor números naturais em seus fatores primos.

Uma distribuidora de gás dividiu a cidade de São Paulo em 200 regiões e estabeleceu o seguinte calendário de entrega por região:

De acordo com o calendário, a região 174 receberá gás na

• A.

  segunda-feira.

• B.

  terça-feira.

• C.

  quarta-feira.

• D.

  quinta-feira.

• E.

  sexta-feira.

Considerando que, para todo número inteiro n, as potências da unidade imaginária i podem ser calculadas através das expressões i4n = 1; i4n+1 = i; i4n+2 = −1 e i4n+3 = −i, é correto afirmar que o valor da soma i−3 + i11 + i207 + i418 é

• A. 0
• B. i
• C. − i
• D. − 1 − i
• E. − 1 + i