Questões de Matemática da Fundação Carlos Chagas (FCC)

• A.

  42

• B.

  46

• C.

  48

• D.

  52

• E.

  56

Para analisar as afirmações seguintes, considere que x é um número par e y é um número ímpar.

I. 3x+ 2y é um número ímpar.

II. 5xy é um número par.

III. x² − y² é um número ímpar.

É correto afirmar que

• A. I, II e III são verdadeiras.
• B. somente uma das afirmações é verdadeira.
• C. somente I e II são verdadeiras.
• D. somente I e III são verdadeiras.
• E. somente II e III são verdadeiras.

• A. negativo.
• B. compreendido entre 0 e 1.
• C. compreendido entre 1 e 2.
• D. compreendido entre 2 e 3.
• E. maior do que 3.

Se N é o menor número inteiro positivo que multiplicado por 77 resulta em um número inteiro cujos algarismos são todos iguais a 9, então a soma dos algarismos de N é

• A. 36
• B. 34
• C. 31
• D. 29
• E. 27

Suponha que em uma parede da área de embarque de uma estação do Metrô há um relógio digital que registra horas, minutos e segundos. Salomé perguntou a um Agente de Estação qual o horário de chegada do próximo trem, e ele, apontando para o relógio digital, respondeu: "O trem chegará no instante em que, nesse relógio, os números que indicam as horas, os minutos e os segundos mudarem, simultaneamente, pela primeira vez." Se no momento em que Salomé fez a pergunta o relógio marcava 07:55:38 (7 horas, 55 minutos e 38 segundos), então ela ainda teve que esperar pelo trem

• A. 4 minutos e 32 segundos.
• B. 4 minutos e 22 segundos.
• C. 4 minutos e 12 segundos.
• D. 3 minutos e 42 segundos.
• E. 3 minutos e 32 segundos.

Valdirene comprou uma barra de chocolate no valor de R$ 4,80 e para pagá-la usou 5 moedas de 50 centavos, 3 de 25 centavos, 9 de 10 centavos e algumas moedas de 5 centavos. Considerando que para fazer o pagamento ela usou apenas esses quatro tipos de moedas, o número de moedas de 5 centavos usadas para completar os R$ 4,80 era

• A. 13
• B. 10
• C. 9
• D. 8
• E. 7

Considere o problema abaixo, proposto a alunos de 6ª série do ensino fundamental.

Para resolver esse problema com competência, seus alunos devem ter desenvolvido, entre outras, a habilidade de

• A.

  estabelecer relação de congruência entre retângulos.

• B.

  determinar as medidas dos lados de um quadrado.

• C.

  compor e decompor figuras geométricas.

• D.

  determinar os divisores de um número natural.

• E.

  identificar os múltiplos de um número natural.

• A.
• B.
• C.
• D.
• E.

Dentre as habilidades que os alunos do 3º ciclo (5ª e 6ª séries) devem desenvolver (PCN-Matemática) salientamos a de utilizar a linguagem algébrica para representar as generalizações inferidas a partir de padrões, tabelas e gráficos em contextos numéricos e geométricos. Para avaliar tal habilidade, um professor propôs a seus alunos o seguinte problema:

Os polígonos que compõem cada figura da seqüência abaixo são triângulos e quadrados.

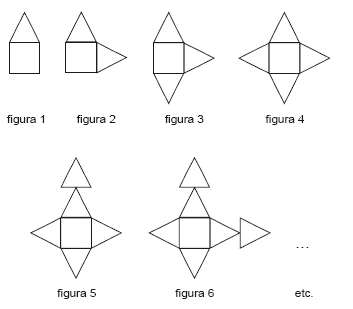
Sabendo como é a figura 10 dessa seqüência, represente o número de triângulos que devem ser acrescentados a ela para se obter a n-ésima figura dessa seqüência, sendo n > 10.

A resposta a essa questão é

• A.

  n

• B.

  n − 10

• C.

  10(n + 10)

• D.

  (n − 10) + (n + 10)

• E.

  (n + 10)²

Considere que na numeração das X páginas de um manual de instruções foram usados 222 algarismos. Se a numeração das páginas foi feita a partir do número 1, então

• A. X < 95
• B. 94 < X < 110
• C. 109 < X < 125
• D. 124 < X < 130
• E. X > 129