Questões de Matemática da Fundação Carlos Chagas (FCC)

Com o objetivo de levar seus alunos a

− eleger as operações que resolvem um problema;
− relacionar diferentes registros de números racionais;
− realizar cálculos com números racionais, por processos pessoais ou convencionais;

um professor propôs a seus alunos a seguinte questão:

Os alunos que tinham desenvolvido aquelas habilidades elegeram, acertadamente, a alternativa

• A.

  A

• B.

  B

• C.

  C

• D.

  D

• E.

  E

Simplificando-se a expressão 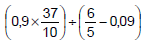 obtém-se um número

• A. ímpar.
• B. divisível por 5.
• C. múltiplo de 6.
• D. negativo.
• E. maior do que 4.

Segundo os PCN de Matemática, quando o conceito de multiplicação é explorado apenas no campo dos números naturais: o efeito da multiplicação é sempre o de aumentar. Assim, para colocar o aluno frente a situações que o faça questionar tal crença, é possível propor a ele, entre outras, uma situação-problema como:

• A.

  Numa loja de artigos de cama, mesa e banho, foram vendidos somente na quinta-feira 37 toalhas de rosto a R$ 7,80 cada uma. Que quantia essa loja recebeu com essa venda?

• B.

  Se eu tinha R$ 32,50 na carteira e fiz apenas uma compra de R$ 12,30, com quanto fiquei na carteira após essa compra?

• C.

  Paulo se encontra no topo de uma escada, a uma altura de 3,5 m em relação ao solo. Se a altura de cada degrau dessa escada é de 0,20 m, então quantos degraus ela tem?

• D.

  Num depósito vazio, são empilhadas 3 caixas com 30 cm, 45,5 cm e 62 cm de altura, respectivamente. Qual é a altura da pilha formada?

• E.

  Uma padaria tem em seu estoque 20 pacotes de 0,250 kg de fermento. De quantos quilos de fermento essa padaria dispõe no estoque?

Assinale a alternativa correspondente ao número de cinco dígitos no qual o quinto dígito é a metade do quarto e um quarto do terceiro dígito. O terceiro dígito é a metade do primeiro e o dobro do quarto. O segundo dígito é três vezes o quarto e tem cinco unidades a mais que o quinto.

• A.

  17942

• B.

  25742

• C.

  65384

• D.

  86421

• E.

  97463

Na página 32 do Referencial de expectativas para o desenvolvimento da competência leitora no ciclo II do ensino fundamental − Matemática, é feita uma crítica à quase que exclusiva proposta que se tem observado em sala de aula de que nas situações-problema oferecidas aos alunos, todos os dados devem ser utilizados e combinados para se obter a resposta que, deve ser única. Nessa crítica, esse Referencial propõe que sejam observados outros aspectos nos problemas propostos, apresentando enunciados que forneçam

• A.

  exatamente 3 dados, para serem combinados entre si durante a resolução.

• B.

  dados supérfluos, isto é, mais dados do que os necessários para a resolução do problema.

• C.

  necessariamente dados de outros campos do conhecimento que não aquele em que o contexto do problema está inserido.

• D.

  representações geométricas dos dados apresentados, para sua melhor concretização.

• E.

  apenas dados numéricos, para que os alunos possam calcular com mais competência.

Alguns relógios utilizam a numeração romana no mostrador como referência à tradição. Observando o mostrador de um desses relógios um aluno notou que a escrita do número 9 era VIIII, e não IX, como seu professor havia ensinado. Sobre essa diferença observada por ele, é correto afirmar que

• A.

  a marcação desse relógio, e de todos os relógios semelhantes a esse, está errada.

• B.

  a marcação refere-se ao sistema de numeração romano anterior à utilização do princípio subtrativo.

• C.

  no sistema romano mais moderno de numeração o 9 pode ser escrito das duas formas.

• D.

  ambas as formas de escrita do 9 não estão de acordo com as regras de formação dos números no sistema romano de numeração.

• E.

  o professor cometeu um deslize ao ensinar errado a escrita do 9 no sistema romano de numeração.

Dados os pares ordenados (a,b) e (x,y), diremos que a operação (a,b)♦(x,y) tem como resultado o par ordenado (a.x, b.y), onde o ponto representa a operação usual de multiplicação. Observe a figura:

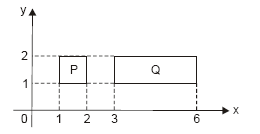
Para que o quadrilátero P se transforme no quadrilátero Q, cada um dos seus pontos, representados pelos pares ordenados (x,y), deve passar pela operação

• A.

  (3,1)♦(x,y)

• B.

  (1,3)♦(x,y)

• C.

  (3,2)♦(x,y)

• D.

  (2,3)♦(x,y)

• E.

  (3,3)♦(x,y)

Considere que a seqüência seguinte é formada pela sucessão natural dos números inteiros e positivos, sem que os algarismos sejam separados.

1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 2 0 ...

O algarismo que deve aparecer na 276^a posição dessa seqüência é

• A. 9
• B. 8
• C. 6
• D. 3
• E. 1

Assinale a alternativa que substitue corretamente a interrogação na seguinte seqüência numérica: 8 12 24 60 ?

• A.

  56

• B.

  68

• C.

  91

• D.

  134

• E.

  168

Um auxiliar judiciário foi incumbido de arquivar 360 documentos: 192 unidades de um tipo e 168 unidades de outro. Para a execução dessa tarefa recebeu as seguintes instruções: 

• todos os documentos arquivados deverão ser acomodados em caixas, de modo que todas fiquem com a mesma quantidade de documentos;
• cada caixa deverá conter apenas documentos de um único tipo.

Nessas condições, se a tarefa for cumprida de acordo com as instruções, a maior quantidade de documentos que poderá ser colocada em cada caixa é

• A.

  8

• B.

  12

• C.

  24

• D.

  36

• E.

  48