Questões de Matemática da Fundação Carlos Chagas (FCC)

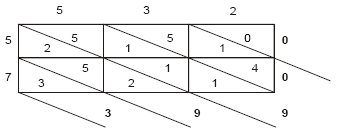
Os hindus, a partir do século VI, efetuavam multiplicações por um método denominado "por quadriculagem". VamosA seguir, adicionam-se os algarismos compreendidos entre as diagonais, da esquerda para a direita e de cima para baixo, colocando-se os resultados no exterior do retângulo maior. Obtém-se, dessa forma, que o resultado de 532 × 75 é 39 900.O quadro seguinte, mostra a multiplicação entre dois números de dois algarismos:O produto obtido nessa multiplicação é igual a mostrá-lo, multiplicando 532 por 75. Para tal, desenhamos um retângulo composto por 6 outros retângulos, dispostos em três colunas (número de algarismos de 532) e duas linhas (número de algarismos de 75). Cada retângulo, dividido pela sua diagonal, traz em cada metade um algarismo do número resultante da multiplicação do algarismo da linha pelo da coluna.

A seguir, adicionam-se os algarismos compreendidos entre as diagonais, da esquerda para a direita e de cima para baixo, colocando-se os resultados no exterior do retângulo maior. Obtém-se, dessa forma, que o resultado de 532 x 75 é 39 900

O quadro seguinte, mostra a multiplicação entre dois números de dois algarismos:

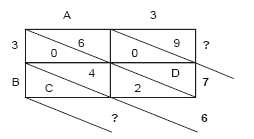
O produto obtido nessa multiplicação é igual a

• A.

  1 679

• B.

  1 426

• C.

  689

• D.

  649

• E.

  619

Leia as afirmações abaixo.

I. A avaliação mediante testes e exames diz muito pouco sobre aprendizagem. Na verdade, os alunos passam em testes para os quais são treinados. É essencial distinguir educação de treinamento.

II. Não conhecer um determinado assunto, seja por falta de interesse, seja por falta de capacidade para aprender esse tema, é grave.

III. O docente está num processo permanente de aprimorar sua prática e nada melhor para isso do que ele próprio conhecer seu desempenho por meio de relatórios dessa prática, feitos pelos alunos.

As afirmações que estão em desacordo com a proposta de avaliação defendida por Ubiratan D'Ambrosio, em seu livro Educação Matemática: da teoria à prática são, APENAS,

• A.

  I e II.

• B.

  II e III.

• C.

  I e III.

• D.

  II.

• E.

  III.

No século IX o matemático Al-Jawhari desenvolveu métodos de resolução de equações, incluindo processos geométricos. Vamos ver um exemplo de representação geométrica para a resolução de uma equação de segundo grau em x. Traçam-se primeiramente um quadrado de lado x unidades e quatro retângulos de lados 2,5 e x unidades.

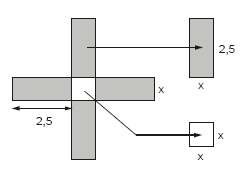
Em seguida, acrescentam-se quatro quadrados de lado 2,5 unidade, obtendo-se dessa forma um quadrado de lado (2,5 + 2,5 + x)

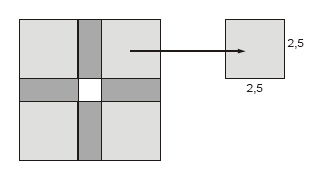
Se esse quadrado tem área de 64 unidades quadradas, o valor de x e uma possível equação para essa representação são

• A.

  4 e x² + 10x = 56

• B.

  4 e x² + 12x = 64

• C.

  3 e 3x² − 55x = 64

• D.

  3 e x² + 10x = 39

• E.

  3 e x² + 8x = −33

Considere as afirmações abaixo.

I. O aluno pode sempre chutar qualquer valor que encontrará, cedo ou tarde a resposta adequada.

II. É uma técnica que estimula a análise do problema, dos dados e dos resultados além de trazer a liberdade de fazer suposições.

III. Ajuda o aluno a selecionar as operações necessárias para resolver o problema e diminui a pressão de obter a resposta correta imediatamente.

Dentre essas afirmações, a adoção da estratégia aproximações sucessivas na resolução de um problema é justificada por

• A.

  II, apenas.

• B.

  III, apenas.

• C.

  II e III, apenas.

• D.

  I e II, apenas.

• E.

  I, II e III.

O artigo "Desenvolvimento da representação algébrica através de diagramas", do livro As idéias da álgebra, organizado por Coxfor, Arthur F. e Shulte, Albert P., os autores, Martin A. Simon e Virginia C. Stimpson traz uma possível representação para o problema: "A soma do número de livros de Jack com o número de livros de Jill é 20. Se Jill perder 3 de seus livros e Jack dobrar a quantidade dos que tem, os dois, juntos, ficarão com 30 livros. Quantos livros tem cada um?"

Um registro algébrico correto para a possível representação é

• A.

  (20 + x) − 3 + 2x = 30

• B.

  20 − x − 3 + 2x = 30

• C.

  17 + 2x = 30

• D.

  17 − x = 30

• E.

  20 − 3 + 2x = 30

Considere o texto apresentado abaixo para responder as questões de números 27 e 28.

Segundo a autora, a resolução apresentada por Dony, utilizou uma determinada estratégia. Essa estratégia está corretamente descrita em:

• A.

  utilização de material dourado.

• B.

  antecipação do resultado.

• C.

  utilização de um algoritmo convencional.

• D.

  reconhecimento de que adição e subtração são operações inversas.

• E.

  busca do complemento do subconjunto em relação ao conjunto universo.

Considere o texto apresentado abaixo para responder as questões de números 27 e 28.

Segundo a autora, a análise da resolução de Dony mostra que:

• A.

  é fundamental que as maneiras convencionais de resolução de problemas, utilizando uma adição ou uma subtração, sejam apresentadas às crianças desde o início do trabalho.

• B.

  encontrar uma estratégia adequada para resolver um problema é algo muito diferente de poder representá- lo através de uma conta convencional.

• C.

  a utilização de algoritmos tradicionais, de adições e/ou subtrações, estimula nas crianças o desejo de diminuir o tempo despendido na resolução de algum problema.

• D.

  na resolução de problemas envolvendo somas e subtrações as crianças utilizam estratégias mentais primárias, que podem ser substituídas, com sucesso, por técnicas convencionais.

• E.

  a maneira mais eficiente de resolver determinado problema sempre exigirá a utilização de um algoritmo convencional.

H. O. Pollack, no livro Aplicações da matemática escolar, trabalho conjunto da Associação Matemática da América, publicado pela Editora Atual, diz, sobre a utilização de modelos matemáticos: Deve-se lembrar também que os modelos matemáticos têm uma multiplicidade de propósitos. Estes vão desde uma compreensão melhor da situação original até a ação decorrente de um resultado da análise. O grau de precisão que se espera de um modelo matemático também varia consideravelmente. As situações da engenharia e da física podem freqüentemente ser modeladas com muita precisão; as situações das ciências sociais podem não se prestar à mesma precisão matemática Não obstante, tais modelos matemáticos não são necessariamente menos importantes ou decisivos enquanto instrumento que proporciona a compreensão e serve de base para a ação.

Com base no texto, é correto o que se afirma em:

• A.

  Os modelos matemáticos têm importância diminuída em ciências sociais porque não apresentam precisão.

• B.

  O propósito de qualquer modelo matemático é único: o de resolver uma situação-problema.

• C.

  Modelos matemáticos podem servir para uma melhor compreensão da situação original.

• D.

  É suficiente a determinação correta das variáveis envolvidas numa situação-problema para uma boa realização de modelos matemáticos.

• E.

  Modelos matemáticos só podem ser utilizados nas ciências exatas e da natureza.

Para representar um número natural qualquer podemos utilizar a letra n. Para representar um número natural ímpar qualquer podemos utilizar a notação 2n + 1. Sendo assim, o resultado de (2n + 1)² sempre será, para qualquer n, um número

• A.

  primo.

• B.

  múltiplo de 3.

• C.

  par.

• D.

  ímpar

• E.

  divisor de 72.

Os pitagóricos, na primeira metade do século VI a.C., segundo Boyer, em seu livro História da Matemática, estudaram os números e os classificaram de acordo com propriedades bem definidas. Assim, denominaram como perfeito o número natural cuja soma de seus divisores, distintos dele mesmo, é igual a ele.

 28 é perfeito porque 28 = 1 + 2 + 4 + 7 + 14

Nicómano, no século II a.C enunciou a seguinte propriedade, relativa aos números perfeitos: se a soma 2⁰+2 +2² +2³ +...+ 2ⁿ = p é um número primo, então 2ⁿ x p é perfeito. Baseado nesta fórmula, o número perfeito e o valor correspondente de p são, respectivamente,

• A.

  256 e p = 13

• B.

  496 e p =31

• C.

  812 e p = 29

• D.

  7116 e p = 593

• E.

  8120 e p =203