Questões de Matemática da Fundação Carlos Chagas (FCC)

Um empréstimo de R$ 50 000,00 deve ser devolvido em 20 prestações mensais, pelo Sistema de Amortização Constante (SAC), Se a taxa de juros cobrada é de 2% ao mês, o valor da décima prestação deverá ser

• A.

  R$ 2 950,00

• B.

  R$ 3 000,00

• C.

  R$ 3 050,00

• D.

  R$ 3 100,00

• E.

  R$ 3 150,00

Num regime de capitalização composta, o montante M, resultante da aplicação de um capital C à taxa porcentual i, por n períodos, é dado pela lei M = C. (1+i). Assim, dados M, C e n, a taxa i pode ser calculada pela expressão:

• A.

  i = (M/C) ^1/N

• B.

  i = ((M-C)/C) ^1/N

• C.

  i = (M 1^/N - C ^1/N) / C ^1/N

• D.

  i = (M ^N - C ^N / C ^N

• E.

  i = ((M+C)/C) ^N

Uma certa indústria fabrica um único tipo de produto, que é vendido ao preço unitário de x reais.Considerando que a receita mensal dessa indústria, em reais, é calculada pela expressão R(x) = 80 000x - 8 000x², então, para que seja gerada uma receita mensal de R$ 200 000, 00, cada unidade do produto fabricado deve ser vendida por:

• A.

  R$ 6,00

• B.

  R$ 5,50

• C.

  R$ 5,00

• D.

  R$ 4,50

• E.

  R$ 4,00

Observando os padrões, os elementos da quinta coluna, respeitando a ordem da tabela, devem ser

• A.

  15, 25, 35, 45

• B.

  15, 25, 40, 50

• C.

  16, 36, 46, 56

• D.

  18, 28, 45, 50

• E.

  20, 30, 40, 50

A soma de dois números inteiros é 924. Juntando 78 a cada um dos números, um dos resultados fica o dobro do outro. O menor desses números é

• A.

  78

• B.

  156

• C.

  231

• D.

  282

• E.

  308

Imagine todas as adições possíveis de duas parcelas distintas que podemos efetuar com os divisores de 36. Dentre as somas obtidas, algumas serão números múltiplos de 5. Os possíveis múltiplos de 5, nesse caso, são

• A.

  3

• B.

  4

• C.

  5

• D.

  6

• E.

  7

Gerald A. Goldin e C.Edwin Mcclintock, em seu artigo "O tema da simetria na resolução de problemas", no livro Resolução de problemas na matemática escolar, dizem: Um aspecto importante da simetria é seu grau de visibilidade, das situações de nitidez às ocultas. Consideraremos as três possibilidades seguintes: a) a simetria se apresenta nítida na representação dada do problema; b) a representação dada requer modificação ou construção auxiliar para revelar a simetria; c) a simetria está oculta ou não é nítida na representação dada, e uma nova representação deve ser construída para exibi-la. Para qualquer dessas possibilidades, a simetria em questão pode ser de reflexão, de rotação e assim por diante.

 De acordo com as idéias contidas nesse parágrafo , podese afirmar corretamente que:

• A.

  Qualquer problema de geometria pode ser resolvido com uso de simetrias.

• B.

  Todas as simetrias são nítidas nos problemas geométricos ou não.

• C.

  As simetrias de rotação não são adequadas para a resolução de problemas.

• D.

  Se uma simetria não é nítida, ela não pode ser usada na resolução de um problema.

• E.

  Uma representação geométrica pode precisar ser modificada para salientar uma simetria.

O livro Timeu, escrito no século IV a .C contém as idéias de Platão sobre 5 poliedros regulares: o tetraedro, o cubo, o octaedro, o dodecaedro e o icosaedro, chamados "poliedros de Platão". Imagine que você seja joalheiro e que possua uma pedra preciosa na forma de um cubo, e deseja esculpi-la. A pedra esculpida terá a forma de um poliedro de Platão cujos vértices, originalmente, eram os pontos centrais das faces do cubo. Quantas faces terá a pedra esculpida?

• A. 4
• B. 6
• C. 8
• D. 12
• E. 20

Sobre um quadrado ABCD, de lado de 4 cm, determinamos os pontos M,N,P e Q de tal forma que AM = BN = CP = DQ = x. A área de MNPQ ,em centímetros quadrados e em função de x, é

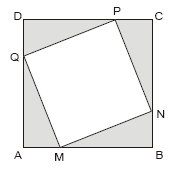
• A.

  2x² – 8x + 16

• B.

  2x² – 4x + 8

• C.

  2x² – 8x + 8

• D.

  x² – 8x + 16

• E.

  x² – 4x + 8

O valor da medida a, em centímetros, no triângulo retângulo MEU é

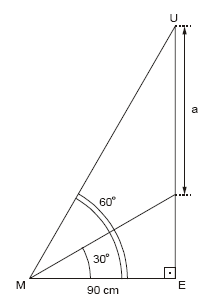
• A.

  

• B.

  

• C.

  

• D.

  

• E.