Questões de Matemática da Fundação Carlos Chagas (FCC)

Um problema clássico consiste em calcular valores de x de modo que 10^x tenha resultados iguais a 1, 2, 3, 4, 5, 6, etc, com boa aproximação.

O valor de x em 10^x=1 é x= 0, pois 10⁰ = 1

Para calcular o valor de x em 10^x = 2, adotaremos a seguinte estratégia: vamos escrever potências de 10 e potências de 2 e procurar, dentre elas, os valores mais próximos.

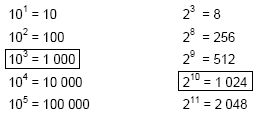
Aproximando 1000 para 1024, teremos:

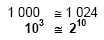
Extraíndo a raiz décima de ambos os membros, ficaremos com o seguinte:

Com base nesse procedimento e considerando a aproximação entre 2 x 10⁴ = 20 000 e 3⁹ = 19 683, o valor de x para 10^x = 3 é

• A.

  0,330

• B.

  0,410

• C.

  0,478

• D.

  0,555

• E.

  0,984

Simplificando a fração 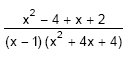 , na qual x ≠ 1 e x ≠ −2 obtém-se

• A.

  

• B.

  

• C.

  

• D.

  x - 1

• E.

  x + 2

Analisando a grande diversidade de respostas que diferentes crianças podem produzir frente ao mesmo problema, Delia Lerner Zunino, em seu livro Matemática na escola: aqui e agora, coloca a questão: Como fazer para que a diversidade constitua-se em um fator positivo para o aprendizado?

Segundo a autora, os três elementos da resposta geral a essa pergunta são:

• A.

  cooperação entre as crianças, confrontação das diversas estratégias, validação das estratégias adotadas.

• B.

  repetição de processos detectados como corretos, análise de expectativas futuras, contextualização.

• C.

  verificação da resposta, confrontação de métodos utilizados, escolha do método considerado mais eficiente.

• D.

  estipulação de tempo dedicado à resolução, eleição do processo que tenha demandado tempo mais curto, aceitação da estratégia eleita como mais eficiente.

• E.

  listagem dos métodos de resolução disponíveis, análise dos métodos realmente utilizados, valorização dos métodos que permitiram acertos.

No conjunto dos números reais a inequação a x 0 x b ≥ − + tem por conjunto-solução { x∈ R / − 3 ≤ x < 4} . Os valores de a e b são, respectivamente,

• A.

  − 3 e − 4

• B.

  − 3 e 4

• C.

  3 e 4

• D.

  3 e − 4

• E.

  3 e − 3

Vamos definir problemas de pesquisa aberta como sendo aqueles em cujo enunciado não há uma estratégia implícita para resolvê-los, nem operações imediatas. Demonstrações de teoremas enquadram-se nessa categoria, assim como questões do tipo "encontre todos...". Leia os problemas:

I. Quais são os números naturais que têm um número ímpar de fatores?

II. Quantos triângulos diferentes, de lados de medidas inteiras, podem ser construídos de modo que o lado maior tenha 5 cm de comprimento? 6 cm? n centímetros?

III. Uma bolsa com moedas de 5, 10 e 25 centavos contém 435 moedas no valor de R$ 43,45 . Há três vezes mais moedas de 10 do que de 25. Quantas moedas de cada tipo estão na bolsa?

IV. Imagine n armários, todos fechados, e n pessoas. Suponha que a primeira pessoa passe e abra todos os armários. Depois, passe uma segunda pessoa e feche um armário sim e o outro não, começando pelo número 2. A terceira pessoa, então, passa e altera o estados das portas dos armários, de três em três, começando pelo número 3 (isto é, se este está aberto, ela o fecha, e vice-versa). Se esse procedimento continuar até que todas as n pessoas passem, quais dentre as portas ficarão abertas?

Com respeito a esses problemas, é INCORRETO afirmar que

• A.

  o problema IV apresenta uma forma instigante de apresentar a mesma situação que aparece no problema I.

• B.

  o problema II é de pesquisa aberta porque propicia ao aluno a experiência de buscar e encontrar um padrão geométrico.

• C.

  o problema III já traz uma estratégia de resolução no enunciado. O obstáculo a vencer é apenas o de traduzir a palavra escrita pela forma matemática apropriada, de maneira a usar as equações adequadas.

• D.

  se reconhece o problema I como de pesquisa aberta pelo tipo de pergunta que faz.

• E.

  apenas o problema IV é de pesquisa aberta.

O gráfico da figura mostra as coordenadas do ponto máximo de uma função de segundo grau do tipo f(x) = ax2 + bx + c

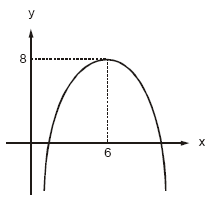
• A.

  4 < x < 6

• B.

  4 < x < 8

• C.

  6 − 2  < x < 6 + 2

• D.

  x < 4 ou x > 8

• E.

  x < 6 − 2  ou x > 6 + 2

A seguinte descrição foi feita por pessoas que cavam poços, explicando como calculam a quantidade de terra a ser extraída na tarefa:

Tomando como base o reconhecimento das relações intraculturais, proposta no livro de Ubiratan D'Ambrosio, Educação Matemática: da teoria à prática, NÃO podemos dizer que a descrição dada

• A.

  pode ser utilizada com os alunos porque mostra que, a partir de soluções para problemas reais, é possível criar novas interpretações e utilizações dessa realidade.

• B.

  é inadequada para ser utilizada com alunos porque mostra uma matemática inexata, embora voltada para problemas reais.

• C.

  é um bom exemplo da ação do homem em direção à sobrevivência, ao saber fazendo e fazer sabendo.

• D.

  mostra que a ação gera o conhecimento, gera a capacidade de explicar, de lidar, de manejar, de entender a realidade.

• E.

  é um procedimento que foi gerado pela necessidade de uma resposta a situações e está sujeito ao um contexto natural, social e cultural.

Dizem os matemáticos que Carl Friedrich Gauss, ainda criança, foi desafiado a calcular a soma dos números inteiros de 1 a 100 e, para resolver a tarefa, utilizou o seguinte raciocínio:

I. Escreveu a soma a ser calculada: 1 + 2 + 3 + 4 + ........ + 97 + 98 + 99 + 100

II. Somou o primeiro com o último termo 1 + 100 = 101

III. Percebeu que a soma de termos eqüidistantes dos extremos era sempre igual à soma do primeiro com o último termo 1 + 100 = 2 + 99 = 3 + 98 = 4 + 97 = ..... = 101

IV. Dividiu o número de termos, 100, por 2 e multiplicou o resultado pela soma do primeiro com o último termo. 100 ÷ 2 = 50 50 x (1 + 100) = 50 x 101 = 5050

Podemos utilizar este raciocínio na determinação de uma fórmula para o cálculo da soma dos números inteiros de 1 a n. Qual é essa fórmula?

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

A autora Delia Lerner de Zunino, em seu livro A matemática na escola: aqui e agora, critica a inconveniência de uma conhecida concepção de ensino e aprendizagem em Matemática. Em qual das afirmações NÃO são apontadas características da concepção criticada pela autora?

• A.

  Ensinar consiste em explicar, aprender consiste em repetir o ensinado até reproduzi-lo fielmente.

• B.

  Ensinar consiste em utilizar muito material concreto e exercitar muito... repetir muitas vezes.

• C.

  As crianças, de modo geral, não são capazes de aprender muitas coisas a partir de sua experiência familiar e social.

• D.

  Os conhecimentos devem ser separados cuidadosamente, para evitar confusões, desse modo as crianças poderão aprender de forma organizada.

• E.

  Ensinar consiste em reconhecer que a aprendizagem de certos conteúdos começa antes do ingresso da criança na escola.

Ao devolver a prova corrigida para a classe, o professor comentou:

 − Pessoal, nessa prova, que valia de 0 a 10, as meninas foram melhor que os meninos, pois a nota média das meninas foi igual a 6,2 enquanto a nota média dos meninos foi igual a 5,9.

A partir da fala do professor, pode-se afirmar que

• A.

  a maioria das meninas tirou nota acima de 6,0.

• B.

  há mais meninas que meninos nessa classe.

• C.

  que todas as meninas podem ter tirado nota igual a 6,2.

• D.

  dentre as meninas a nota mais freqüente foi 6,2.

• E.

  a soma das notas de todos os meninos é menor que a soma das notas de todas as meninas.