Questões de Matemática da Fundação Carlos Chagas (FCC)

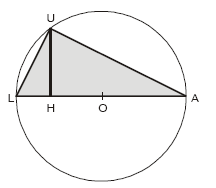
No triângulo LUA, o lado LA é diâmetro do círculo de centro O. A altura UH do triângulo divide o segmento LA em segmentos LH e HA, que medem, respectivamente, 8,0 cm e 32 cm. A medida UH, em centímetros, é igual a

• A.

  8,0

• B.

  10

• C.

  12

• D.

  16

• E.

  18

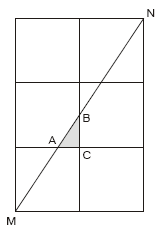
Na malha da figura, cada quadrado menor tem 6,0 cm de lado. A área do triângulo ABC, determinado pela diagonal MN é , em centímetros quadrados, igual a

• A.

  3,0

• B.

  5,0

• C.

  7,5

• D.

  8,0

• E.

  10,0

Os egípcios calculavam inclinações usando razões, de modo semelhante ao que fazem hoje nossos arquitetos.Se o seqt ou cotg 57° é 65%, então, com respeito à altura do morro, é verdade que Dessa forma eram estabelecidas, por exemplo, inclinações de telhados, rampas, etc, calculadas pelo quociente entre o afastamento horizontal e a elevação vertical, razão conhecida como seqt. Se, por exemplo, for considerada uma elevação vertical de 20 m para um deslocamento horizontal de 100 m, a razão a ser considerada é 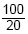 , que corresponde ao valor da cotangente do ângulo de elevação.

Imagine que se queira calcular a altura de um morro de difícil acesso a seu pé, como o que está desenhado abaixo, e que foi possível estabelecer as medidas indicadas.

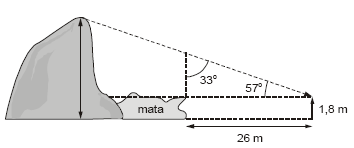
Se o seqt ou cotg 57º é 65%, então, com respeito à altura do morro, é verdade que

• A.

  os dados são insuficientes para calculá-la.

• B.

  é 42,9 m.

• C.

  é 16,9 m.

• D.

  para calculá-la é necessário saber o valor de cotg 33° e não o de cotg de 57°.

• E.

  é 44,7m.

Galileu Galilei, físico, astrônomo e escritor italiano, que viveu de 1564 a 1642, estudou, dentre outras coisas,Se a distância x na figura for igual a 2,0 cm, a medida (x + y) para que a teoria de Galileu esteja correta é igual a corpos em movimento acelerado. Observando bolas rolarem por planos inclinados muito lisos, quase sem atrito, Galileu percebeu que uma bola colocada no alto do plano inclinado descia acelerando de maneira que a distância que percorria era diretamente proporcional ao quadrado do tempo de descida. A figura representa a descida de uma bola que foi "fotografada" em três instantes. O intervalo de tempo decorrido entre o instante inicial e o instante 1 é igual ao intervalo de tempo decorrido entre os instantes 1 e 2.

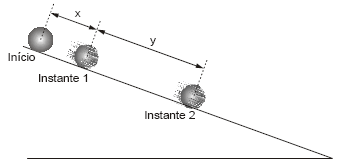
Se a distância x na figura for igual a 2,0 cm, a medida (x+y) para que a teoria de Galileu esteja correta é igual a

• A.

  4,0 cm

• B.

  6,0 cm

• C.

  8,0 cm

• D.

  10 cm

• E.

  12 cm

Um retângulo é chamado de "Áureo" quando a razão entre as medidas do lado maior e menor é igual à razão entre a soma das medidas dos lados e o lado maior. Se a figura representa um retângulo áureo, a medida do lado maior é, em centímetros, igual a

• A.

  6

• B.

  

• C.

  

• D.

  8

• E.

  

Um fazendeiro pretende plantar dois tipos de mudas de árvores, X e Y, em uma grande quantidade de terra disponível. Na figura é possível ver a área que deve ser destinada a uma unidade de cada muda.

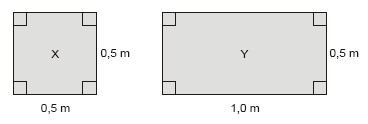
Chamando, respectivamente, de n e de m as quantidades de mudas dos tipos X e Y que serão plantadas, a área W ocupada pela plantação dos dois tipos de mudas poderá ser expressa corretamente por:

• A.

  W = (n + m).(X + Y)

• B.

  W = (0,25 + X)n + (0,5 + Y)m

• C.

  W = 0,25nX + 0,5mY

• D.

  W = 0,25n + 0,5m

• E.

  W = 0,25X + 0,5Y

No livro Os elementos, escrito por Euclides no século III a .C., há a seguinte definição para a reta:

"Linha reta é aquela, que está posta igualmente entre as suas extremidades."

Observando o estudo da geometria contemporânea, podemos dizer que essa definição:

• A.

  é igual à usada atualmente.

• B.

  indica que a reta não é limitada.

• C.

  afirma que reta é o que tem comprimento sem largura.

• D.

  parte da definição de ponto, dada por Euclides nos Elementos: Ponto é o, que não tem partes, ou o que não tem grandeza alguma.

• E.

  aproxima-se da definição atual de segmento.

No papiro de Ahmes, antigo documento escrito pelos Egípcios, foram registrados vários problemas matemáticos. O problema de número 48 mostra uma comparação entre a área de um círculo e a área de um octógono não regular, construído dentro de um quadrado.

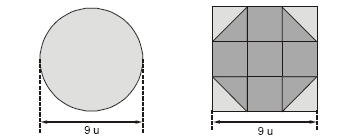
Numa unidade de medida qualquer, u, o círculo tem diâmetro 9u, e o lado do quadrado que dá origem ao octógono mede também 9u. Considerando que as duas áreas, do círculo e do octógono, sejam iguais, foi possível calcular o valor de π. Ubiratan D'Ambrosio, em seu livro Educação Matemática: da teoria à prática, discorre sobre o papel da história da matemática no ensino. Sobre trabalhar com os alunos o método do papiro de Ahmes, está em completo acordo com as reflexões de Ubiratan Dámbrósio na obra citada a afirmação:

• A.

  Não vale a pena conhecer historicamente pontos altos da matemática de ontem porque, na melhor das hipóteses, isto apenas orienta o aprendizado e o desenvolvimento da matemática de hoje.

• B.

  Não vale a pena, porque o valor encontrado para π é 3,11 e , portanto, não muito próximo do valor correto.

• C.

  Como em outros assuntos, conhecer o método traz elementos para se perceber como teorias e práticas matemáticas foram criadas, desenvolvidas e utilizadas num contexto específico de sua época.

• D.

  Do ponto de vista de motivação contextualizada, a matemática que se ensina na escola de hoje é morta. Poderia ser tratada como fato histórico. Sendo assim, para que mostrar um método tão antigo de cálculo?

• E.

  Algo da matemática do passado serve para hoje, mas, muito pouco, e, mesmo assim, em linguagem e codificação moderna. Procedimentos e métodos antigos devem ser completamente banidos do ensino da matemática.

Na sexta noite de sonhos com o diabo Teplotaxl, no livro O diabo dos números, de Hans Manus Enzensberger, o personagem Robert conhece a seqüência de Fibonacci. Os retângulos desenhados têm padrões que estão relacionados com essa seqüência.

Se cada quadradinho tem uma unidade de área, quantas unidades terá a soma das áreas dos dois próximos retângulos a serem desenhados?

• A.

  40

• B.

  55

• C.

  104

• D.

  140

• E.

  144

Estão corretamente identificadas possíveis transformações isométricas de serem realizadas com uma figura plana em:

• A.

  ampliação, reflexão e translação.

• B.

  reflexão, translação e redução.

• C.

  reflexão, rotação e translação.

• D.

  rotação, redução e ampliação.

• E.

  translação, redução e ampliação.