Questões de Matemática da Fundação Carlos Chagas (FCC)

Suponha que, na construção de um duto para escoamento da água de um reservatório é usada uma peça feita de alumínio maciço, obtida de um corte de um paralelepípedo retângulo, gerando uma canaleta semicircular, conforme é mostrado na figura abaixo.

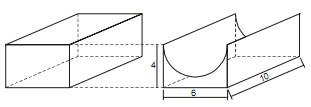
Considerando que as dimensões indicadas na figura são dadas em metros e usando a aproximação π= 3,1, então, se a densidade do alumínio é 2,6 g/cm³, a massa dessa peça em toneladas, é igual a

• A.

  2,613.

• B.

  3,213.

• C.

  26,13.

• D.

  32,13.

• E.

  261,30.

A receita diária de uma locadora de DVDs é dada por R = 5 p² − 80 p, em que p é o preço cobrado por vídeo alugado. Qual deve ser o valor mínimo cobrado por DVD alugado para que a receita diária seja de R$ 180,00?

• A.

  R$ 4,00.

• B.

  R$ 6,00.

• C.

  R$ 8,00.

• D.

  R$ 10,00.

• E.

  R$ 12,00.

A Agência Nacional de Energia Elétrica (Aneel) é responsável, entre outras coisas, por definir tarifas que cada concessionária cobrará por kwh (quilowatt-hora) consumido, sem considerar os impostos. A tabela mostra as tarifas que deverão ser cobradas pela Eletropaulo Metropolitana Eletricidade de São Paulo S.A. para algumas faixas de consumo.

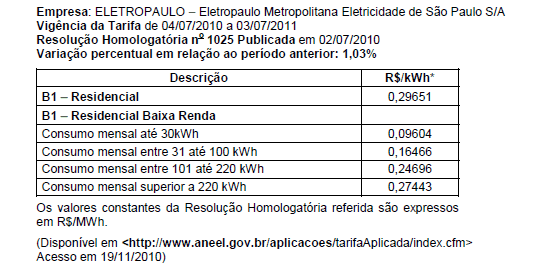
Se uma residência que não seja de baixa renda gastou 300 kWh, que quantia representa o gasto com a tarifa?

• A.

  R$ 28,81.

• B.

  R$ 49,40.

• C.

  R$ 74,09.

• D.

  R$ 84,01.

• E.

  R$ 88,95.

O número de horas trabalhadas em uma empresa determina seu faturamento, em reais e sua produção, em número de peças. O faturamento f é dado por f = 150 t + 1 200, e o número de peças produzidas p, por p = 6 t, em que o parâmetro t são as horas trabalhadas. Qual o faturamento e o número de peças produzidas em 8 horas de trabalho?

• A.

  f = 1 200; p = 48.

• B.

  f = 48; p = 2 400.

• C.

  f = 48; p = 1 200.

• D.

  f = 2 400; p = 48.

• E.

  f = 48; p = 12 000.

Uma empresa está montando pacotes com brindes promocionais para presentear seus clientes. Veja a composição de dois tipos de pacotes montados:

I. Uma garrafa de vinho e dois panetones;

II. Duas garrafas de vinho e um panetone.

Determine o valor gasto pela empresa pela compra de uma garrafa de vinho e um panetone, sabendo que o pacote tipo I custa R$ 50,00 e o pacote tipo II custa R$ 55,00.

• A.

  R$ 15,00.

• B.

  R$ 20,00.

• C.

  R$ 25,00.

• D.

  R$ 30,00.

• E.

  R$ 35,00.

A sexta parte de 12⁶⁶ é

• A.

  2⁶⁶.

• B.

  12¹¹.

• C.

  12⁵⁰.

• D.

  21²⁰. 3⁶⁵.

• E.

  21³¹. 3⁶⁵.

Para demonstrar seus conhecimentos matemáticos Lucas disse para Enrique:

O quadrado da minha idade somado com sua metade resultará em um século e meio. Você é capaz de dizer qual é a minha idade atual?

Enrique, para surpresa de Lucas, respondeu corretamente após alguns minutos: Você tem

• A.

  10 anos.

• B.

  11 anos.

• C.

  12 anos.

• D.

  13 anos.

• E.

  14 anos.

Os táxis de uma cidade cobram um valor fixo pela bandeirada e mais uma taxa por quilômetro rodado. Sendo B, Q e T, respectivamente, os valores (em reais) da bandeirada, do quilômetro rodado e do total pago de tarifa no táxi após uma viagem de X quilômetros, é correto afirmar que

• A.

  T − B é diretamente proporcional à X, sendo que a constante de proporcionalidade é Q.

• B.

  T é diretamente proporcional à X, sendo que a constante de proporcionalidade é Q.

• C.

  T é diretamente proporcional à X, sendo que a constante de proporcionalidade é B.

• D.

  T é inversamente proporcional à X.

• E.

  X . Q − T é inversamente proporcional à B.

Sendo x um número real, a equação 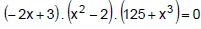 possui apenas

• A.

  três soluções racionais e nenhuma irracional.

• B.

  três soluções irracionais e nenhuma racional.

• C.

  duas soluções racionais e duas irracionais.

• D.

  quatro soluções racionais e nenhuma irracional.

• E.

  cinco soluções racionais e nenhuma irracional.

Chama-se distância de frenagem a distância d que um veículo percorre quando o motorista aciona o freio.

Para que se criem regras de segurança adequadas, testes são realizados. Dessa forma, observa-se uma relação entre a distância de frenagem (d) e a velocidade do automóvel (v) no instante do acionamento dos freios.

A tabela abaixo indica alguns resultados obtidos nos testes realizados.

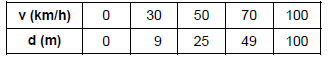
Conclui-se que a distância de frenagem é diretamente proporcional ao quadrado da velocidade no instante que se acionam os freios. Pode-se afirmar que a constante de proporcionalidade é

• A.

  100.

• B.

  75.

• C.

  50.

• D.

  1/50.

• E.

  1/100.