Questões de Matemática da Fundação Carlos Chagas (FCC)

O gráfico cartesiano abaixo representa uma função g(x) = 2x² + kx + m, em que k e m são números reais.

O resultado de m + k é igual a:

• A.

  −26.

• B.

  −14.

• C.

  −12.

• D.

  −8.

• E.

  −6.

Considere que os números inteiros que aparecem na tabela abaixo foram dispostos segundo determinado padrão.

Mantido indefinidamente esse padrão, se X é o número que pertence à 65ª linha e à 3ª coluna e Y o que pertence à 54ª linha e à 5ª coluna, então X + Y

• A.

  não pertence a essa tabela.

• B.

  pertence à primeira coluna.

• C.

  pertence à segunda coluna.

• D.

  é maior que 3 000.

• E.

  é menor que 1 500.

Ana Maria decidiu preparar uma torta cuja receita indicava 200 gramas de chocolate em barra. Em sua dispensa, havia uma barra de 350 gramas, mas ela não dispunha de uma balança para pesar a quantidade necessária. Então, ela decidiu dividir a barra em partes iguais e pegar a quantidade de partes que correspondessem a 200 gramas. Dentre os esquemas abaixo, em que os retângulos escuros correspondem às partes da barra de chocolate usadas por Ana Maria, aquele que representa os 200 gramas pedidos na receita é

• A.
• B.
• C.
• D.
• E.

Sendo x e y números reais tais que y = − 6x² +11x − 4 , o valor mínimo de x para o qual o valor correspondente de y é máximo é

• A.

  2/3.

• B.

  3/4.

• C.

  5/6.

• D.

  11/12.

• E.

  1.

Considere que os termos da sequência (1, 2, 4, 5, 11, 12, 26, 27, 57, 58, . . .) foram obtidos segundo uma lei de formação. Segundo essa lei, o décimo quinto termo é um número

• A.

  maior que 500.

• B.

  divisível por 6.

• C.

  quadrado perfeito.

• D.

  múltiplo de 4.

• E.

  primo.

Apesar de ser um dos mais famosos matemáticos Bhaskara, que viveu no séc. XII, não contribuiu diretamente na elaboração da fórmula que leva seu nome. Na história da Matemática podemos encontrar egípcios, babilônios, gregos, outros hindus e chineses. Entre eles podemos destacar, Euclides, Diophanto, Al-Khowârizmî, Zhu Shijie (também chamado Chu Shih-Chieh).

No século XIX o método foi redescoberto por Willian George Horner e Theophilus Holdred e, um pouco antes por Paolo Ruffini. O que ficou conhecido como método de Horner, já tinha sido antecipado por Isaac Newton em 1669. No século XVI, François Viéte utilizou-se de simbolismo para representar esse processo.

A contribuição atribuída a Bhaskara serve para

• A.

  determinar quais são os números primos compreendidos entre 1 e 100.

• B.

  determinar medidas proporcionais em figuras semelhantes.

• C.

  relacionar as medidas dos catetos com a hipotenusa de um triângulo retângulo.

• D.

  a resolução de uma equação de 2o grau.

• E.

  determinar o máximo divisor comum entre dois ou mais números.

A professora de uma sala de aula de 8o ano resolveu fazer um levantamento das alturas de seus 35 alunos para compará-las com sua média aritmética. Percebeu que todos os números encontrados pertencem ao conjunto dos números

• A.

  inteiros, mas não ao conjunto dos números naturais.

• B.

  racionais não negativos.

• C.

  reais não positivos.

• D.

  racionais não positivos.

• E.

  complexos, mas não ao conjunto dos números reais.

Ao discutir um conteúdo matemático com seus alunos, o professor propôs o seguinte problema:

Ana e Bruno, juntos, têm mais do que 3 litros de tinta branca. A diferença entre o triplo da quantidade de tinta de Bruno e o dobro da quantidade de tinta de Ana, nessa ordem, é maior que meio litro. Apresente uma representação geométrica das soluções dos pares ordenados (A,B) que indiquem todas as possibilidades da quantidade A de tinta branca de Ana, em litros, e da quantidade B de tinta branca de Bruno, em litros.

Para que a questão proposta possa ser resolvida com máximo rigor matemático, os alunos terão que trabalhar com

• A.

  potências e árvore de possibilidades.

• B.

  equação geral da circunferência e de elipse.

• C.

  sistema de equações e representação dos pares (A,B) em tabelas.

• D.

  sistema de inequações e sua representação no plano cartesiano.

• E.

  conservações de unidades de medidas e gráfico de setores.

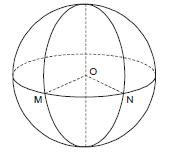
O desenho representa a esfera terrestre em que foram assinalados 2 pontos M e N sobre a linha do equador. Se o ângulo MÔN mede 45°, qual é, em função do raio r da Terra, a medida do arco MN?

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Observe duas circunferências representadas no plano cartesiano. A circunferência C₁ é tangente aos dois eixos em x = 3 e y = 3, enquanto a circunferência C₂ é tangente aos eixos em x = −5 e y = 5.

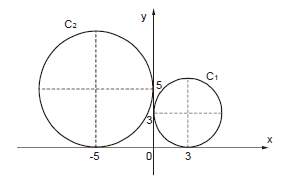
A circunferência C₂ sofrerá uma translação horizontal e uma vertical, de modo que, ao final, seu centro coincidirá com o centro da circunferência C₁. Qual das alternativas contém as translações que a circunferência C₂ executará?

• A.

  

• B.

  

• C.

  

• D.

  

• E.