Questões de Matemática da Fundação Carlos Chagas (FCC)

Um professor pediu que seus alunos desenhassem (com régua e compasso) em uma cartolina dura e de material com massa uniformemente distribuída um triângulo escaleno qualquer. Em seguida, o professor pediu que os alunos recortassem o triângulo e marcassem nele (usando régua e compasso) os seguintes pontos:

− ponto equidistante dos vértices do triângulo (P);

− ponto equidistante dos lados do triângulo (Q);

− centro de massa do triângulo (R).

Sabendo-se que:

− Baricentro é o encontro das três medianas;

− Circuncentro é o encontro das três mediatrizes;

− Incentro é o encontro das três bissetrizes;

− Ortocentro é o encontro das três alturas.

Alunos que resolveram corretamente o problema proposto pelo professor marcaram P, Q e R por meio das construções, respectivamente, do

• A.

  baricentro, incentro e circuncentro.

• B.

  circuncentro, incentro e ortocentro.

• C.

  ortocentro, incentro e circuncentro.

• D.

  circuncentro, incentro e baricentro.

• E.

  incentro, circuncentro e baricentro.

Um artista esculpe um cubo de pedra e, em seguida, escava em uma das faces um cone circular reto. A base circular do cone está inscrita na face do cubo, e o vértice do cone coincide com o ponto de encontro das diagonais da face oposta à face escavada do cubo. Uma planificação adequada da superfície externa dessa obra é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Aplicando o Teorema de Pitágoras é possível determinar a

• A.

  medida do volume de um cubo conhecendo-se a medida de sua aresta.

• B.

  medida da área de um retângulo conhecendo-se as medidas de seus lados.

• C.

  distância entre dois pontos quaisquer de uma circunferência conhecendo-se suas coordenadas.

• D.

  constante de proporcionalidade entre duas figuras semelhantes.

• E.

  medida da diagonal de um quadrado conhecendo-se a medida de seu lado e vice-versa.

Os termos da sequência (25; 22; 11; 33; 30; 15; 45; 42; 21; 63; . . .) são obtidos segundo um determinado padrão. De acordo com esse padrão o décimo terceiro termo da sequência deverá ser um número

• A.

  não inteiro.

• B.

  ímpar.

• C.

  maior do que 80.

• D.

  divisível por 4.

• E.

  múltiplo de 11.

Em um determinado período, uma indústria fabrica um produto e consegue vender todas as unidades produzidas. O custo total correspondente (CT) é dado por CT = 10q unidades monetárias, em que q é o número de unidades produzidas e vendidas. A demanda para esse produto obedece a relação p =−0,125q + 25, sendo p o preço unitário de venda do produto em unidades monetárias. O valor do lucro máximo total, nesse período, alcançado pela indústria é, em unidades monetárias, igual a

• A.

  450.

• B.

  650.

• C.

  900.

• D.

  1.050.

• E.

  1.350.

O gráfico a seguir representa a função f, de domínio real, dada pela lei f(x) = ax² + bx + c.

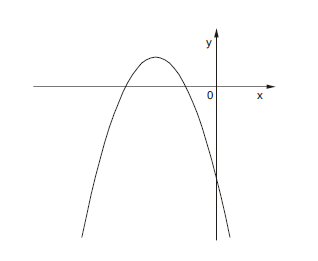
Sabendo que a, b e c são constantes, é correto concluir que

• A. a < 0, b < 0 e c < 0
• B. a < 0, b < 0 e c < 0
• C. a < 0, b > 0 e c < 0
• D. 0
• E. a > 0, b < 0 e c < 0

Uma variável real y depende de uma variável real x de forma que, sempre que x aumenta 4 unidades, o valor de y aumenta 2 unidades. Dentre os gráficos abaixo, o único que pode representar a relação de dependência dessas duas variáveis é

• A.
• B.
• C.
• D.
• E.

Na tela de um videogame de bolso, um ponto percorre em 4,5 segundos os lados não paralelos e a base menor de um trapézio isósceles, com velocidade constante de 2 cm/s. Sabe-se que o ângulo agudo entre um lado não paralelo do trapézio e a base maior mede 30º, e que a altura do trapézio mede 2 cm. Nas condições dadas, a medida da base menor do trapézio, em cm, é

• A.

  1.

• B.

  0,8.

• C.

  1,2.

• D.

  1,5.

• E.

  2.

Certo dia em que faltou luz em uma cidade, duas velas de mesma altura e mesma forma foram acesas num mesmo istante. Relativamente a essas duas velas, sabe-se que: suas chamas se mantiveram acesas até que fossem totalmente consumidas; ambas queimaram em velocidades constantes; uma delas foi totalmente consumida em 4 horas, enquanto que a outra o foi em 3 horas. Assim sendo, a partir do instante em que as velas foram acesas, quanto tempo foi decorrido até que a medida da altura de uma das velas ficou igual ao triplo da medida da altura da outra?

• A.

  2 horas.

• B.

  2 horas e 15 minutos.

• C.

  2 horas e 40 minutos.

• D.

  3 horas.

• E.

  3 horas e 20 minutos.

Considere as seguintes afirmações:

I. Se x é um número inteiro, então .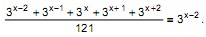

II. 0,36363612480215 . . . é um número racional.

III. A expressão (8,8 X 10^-9). (6,025 X 10⁶) é equivalente a 5,305 X 10^-2.

Relativamente a essas afirmações, é correto afirmar que

• A.

  I, II e III são verdadeiras.

• B.

  apenas I e III são verdadeiras.

• C.

  apenas II e III são verdadeiras.

• D.

  apenas uma é verdadeira.

• E.

  I, II e III são falsas.