Questões de Matemática da Fundação Carlos Chagas (FCC)

Em meio a uma conversa com seu amigo Astolfo, Pablo comentou:

- À meia noite de ontem meu relógio marcava a hora certa e, a partir de então, passou a atrasar 12 minutos por hora, até que, há 8 horas atrás, quando marcava 4 horas e 48 minutos, parou por completo. Você pode me dizer que horas são agora?

Considerando que, nesse instante, o relógio de Astolfo marcava a hora certa e ele respondeu corretamente à pergunta feita, a resposta que Pablo recebeu foi:

• A.

  12 horas e 48 minutos.

• B.

  13 horas.

• C.

  13 horas e 24 minutos.

• D.

  14 horas.

• E.

  14 horas e 36 minutos.

É sabido que o Real, moeda oficial brasileira, é operacionalizado no sistema decimal de numeração, ou seja,

Considerando que, em visita a esse país, uma pessoa gastou 12 432 suns em compras diversas, então, para que ela possa gastar a quantia equivalente em reais são suficientes

• A.

  18 cédulas de 50 reais.

• B.

  16 cédulas de 50 reais e 20 de 10 reais.

• C.

  16 cédulas de 50 reais e 5 de 20 reais.

• D.

  5 cédulas de 100 reais e 92 de 5 reais.

• E.

  3 cédulas de 100 reais, 20 de 20 reais e 29 de 10 reais.

Assinale, entre os pontos abaixo, aquele que satisfaz ao seguinte sistema de inequações: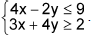

• A.

  (2, 6).

• B.

  (1, −10).

• C.

  (0, 0).

• D.

  (10, −1).

• E.

  (5, −2).

Seguindo as mesmas instruções do professor, encontrando os valores de b e c no terno pitagórico (11, b, c), é correto dizer que b + c é igual a

• A.

  121.

• B.

  131.

• C.

  141.

• D.

  151.

• E.

  189.

Os termos da sequência (12, 15, 9, 18, 21, 15, 30, 33, 27, 54, 57, . . .) são sucessivamente obtidos através de uma lei de formação. Se x e y são, respectivamente, o décimo terceiro e o décimo quarto termos dessa sequência, então:

• A.

  x . y = 1530

• B.

  y = x + 3

• C.

  x = y + 3

• D.

  y = 2x

• E.

  x/y = 33/34

Dados, num plano cartesiano, as coordenadas dos vértices de um triângulo retângulo, a demonstração de que o ponto médio da hipotenusa está a uma mesma distância de cada um dos vértices deste triângulo envolve apenas o uso

• A.

  dos coeficientes angular e linear da reta.

• B.

  das coordenadas do baricentro e do coeficiente linear da reta.

• C.

  da condição de alinhamento entre dois pontos e das coordenadas de ponto médio de um segmento.

• D.

  das coordenadas de ponto médio de um segmento e da fórmula de distância entre dois pontos.

• E.

  das equações reduzida e segmentária da reta.

Seja ∆ a operação definida por u^∆ = 3 − 5u, qualquer que seja o inteiro u. Calculando (-2)^∆ + (2^∆)^∆  obtém-se um número compreendido entre:

• A.

  −20 e −10

• B.

  −10 e 20

• C.

  20 e 50

• D.

  50 e 70

• E.

  70 e 100

• A.

  12.

• B.

  13.

• C.

  14.

• D.

  15.

• E.

  16.

Em uma prova com X questões a nota máxima é 10,0 e odas elas têm o mesmo valor. Suponha que um aluno acerte 18 das 32 primeiras questões e, das restantes, ele acerte 40%. Assim sendo, se esse aluno tirou nota 5,0 nessa prova, então X é um número

• A.

  múltiplo de 4.

• B.

  divisível por 17.

• C.

  menor que 50.

• D.

  primo.

• E.

  quadrado perfeito.

O gráfico a seguir representa uma função polinomial do 1º grau.

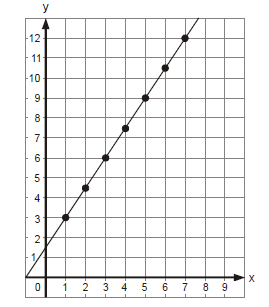
Com relação à sequência de pontos (x,y) marcados na reta, é correto afirmar que mantém associação direta com uma progressão

• A.

  geométrica de razão 3.

• B.

  geométrica de razão igual ao coeficiente angular da reta que passa pelos pontos.

• C.

  aritmética de razão igual ao seno do ângulo de inclinação da reta que passa pelos pontos.

• D.

  aritmética de razão igual ao coeficiente angular da reta que passa pelos pontos.

• E.

  aritmética de razão igual a 3.