Questões de Matemática da Fundação Carlos Chagas (FCC)

Os valores limites da função seno são:

• A.

  −2 a +2

• B.

  0 a +2

• C.

  0 a +1

• D.

  −1 a +1

• E.

  −Q a +Q

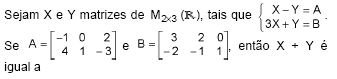
• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Analise a seqüência abaixo.

Nessas condições, quantas vezes o algarismo 1 aparece no resultado de 12 345 678 × 9 + 9?

• A.

  9

• B.

  10

• C.

  11

• D.

  12

• E.

  13

Considere o sistema linear S: 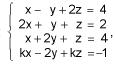    em que x, y e z são incógnitas reais.

Se S admite uma única solução, então a constante k é um número real

• A.

  negativo.

• B.

  quadrado perfeito.

• C.

  divisível por 3.

• D.

  primo.

• E.

  racional não inteiro.

Considere que todos os números inteiros ímpares e positivos podem ser sucessivamente dispostos em linhas e colunas, na forma como é mostrado abaixo.

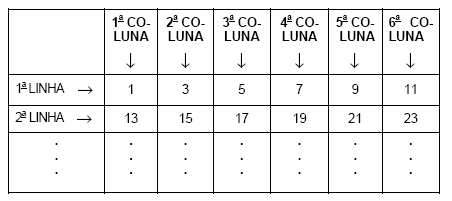
Se fosse possível completar essa tabela, então na quarta coluna e na tricentésima vigésima sétima linha apareceria o número

• A.

  4 021

• B.

  4 015

• C.

  3 937

• D.

  3 919

• E.

  3 847

Na sucessão seguinte os números foram colocados obedecendo a um determinado padrão.

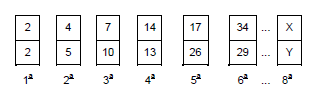
Segundo esse padrão, os números que substituem corretamente X e Y na 8a posição são tais que X + Y é igual a

• A.

  95

• B.

  135

• C.

  147

• D.

  149

• E.

  157

Considere a seguinte seqüência de igualdades:

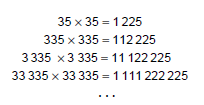
Com base na análise dos termos dessa seqüência, é correto afirmar que a soma dos algarismos do produto 33 333 335 × 33 333 335 é

• A.

  28

• B.

  29

• C.

  30

• D.

  31

• E.

  33

Em uma urna A (azul) foram colocadas 3 000 bolas azuis e em urna V (vermelha) foram colocadas 2 000 bolas vermelhas. A seguir foram feitas 3 operações:

1º - Retiraram-se 50 bolas da urna V (evidentemente todas vermelhas) que foram colocadas bem misturadas na urna A. A seguir retiraram-se aleatoriamente 50 bolas dessa mesma urna A e colocaram- nas, bem misturadas, na urna V.

2º - Retiraram-se 100 bolas da urna A que foram bem misturadas às bolas da urna V. Retiraram-se, agora, 100 bolas da urna V e colocaram-nas na urna A, cuidando de misturá-las bem.

3º - Retiraram-se agora 200 bolas da urna V que foram colocadas na urna A, sempre misturando-as bem. A seguir, retiraram-se (sempre aleatoriamente) 200 bolas da urna A colocando-as, bem misturadas, na urna V.

Tendo feito essas três operações é correto afirmar que

• A.

  há mais bolas azuis na urna V que bolas vermelhas na urna A, pois como o número de bolas azuis é maior, há uma probabilidade maior.

• B.

  há mais bolas vermelhas na urna A que bolas azuis na urna V, pois a concentração favorece esse desequilíbrio.

• C.

  nada se pode afirmar pois, se foram bem misturadas a cada operação, não se pode prever o resultado.

• D.

  há tantas bolas azuis na urna V quanto bolas vermelhas na urna A, após essas operações.

• E.

  seria necessária uma quarta operação para chegarmos a alguma conclusão, começando com bolas da urna V para a urna A.

Em um anfiteatro há 8 poltronas dispostas em duas linhas e quatro colunas, da forma como é mostrado na figura seguinte:

Pretende-se acrescentar outras 55 poltronas às já existentes, preservando o padrão anterior, ou seja, em linhas e colunas, e de modo que o número de colunas exceda o de linhas em duas unidades. Após isso, a nova disposição das poltronas no anfiteatro ficará com

• A.

  seis colunas.

• B.

  cinco linhas.

• C.

  sete colunas.

• D.

  seis linhas.

• E.

  nove colunas.

Um ladrão encontrou na joalheria que invadiu uma sacola com diamantes que parecia ser toda a fortuna do proprietário. Teve a intenção de levar todos os diamantes, porém com "dor na consciência" levou a metade da quantidade e mais dois diamantes.

Um segundo ladrão, encontrando a porta arrombada fez, a seguir, o mesmo que o primeiro: levou metade do que havia sobrado de diamantes e mais dois diamantes.

E isso aconteceu igualmente com um terceiro ladrão, que sucedeu o segundo, e com um quarto, que sucedeu ao terceiro, todos levando a metade dos diamantes que encontravam e mais dois. Ao raiar do dia o joalheiro viu a porta entreaberta e correu até a sacola onde havia um único e solitário diamante.

A quantidade de diamantes que havia na sacola antes do primeiro ladrão entrar era

• A.

  44

• B.

  60

• C.

  76

• D.

  96

• E.

  108