Questões de Matemática da Instituto de Planejamento e Apoio ao Desenvolvimento Tecnológico e Científico (IPAD)

Um carro só pode carregar até 25 pessoas por viagem. No mínimo, quantas viagens são necessárias para transportar 1005 pessoas?

Assinale a alternativa correta:

• A. 4 viagens.
• B. 5 viagens.
• C. 40 viagens.
• D. 41 viagens.
• E. 45 viagens.

Mário tinha como tarefa fiscalizar um certo número de empresas, e resolveu distribuir a tarefa em três dias. No primeiro dia ele fiscalizou a metade das empresas, e no segundo dia fiscalizou a metade do número de empresas que havia fiscalizado no dia anterior. Que fração do número total de empresas Mário teve que fiscalizar no terceiro dia para cumprir a tarefa?

• A.
• B.
• C.
• D.
• E.

Em um programa de perguntas e respostas na TV, a cada resposta certa o concorrente ganha o dobro do valor que tinha antes. Na primeira resposta certa ele ganha 10 reais, na segunda ganha 20 reais, na terceira 40 reais, e assim por diante. Se em uma partida Joana ganhou R$ 1 270,00, quantas respostas ela acertou?

• A.

  7 respostas.

• B.

  9 respostas.

• C.

  12 respostas.

• D.

  15 respostas.

• E.

  17 respostas.

Em uma avenida, foram colocados 12 postes de iluminação, distantes 300 metros um do outro, sendo que o primeiro poste foi colocado no início da avenida, e o último poste foi colocado no fim da avenida. Qual o comprimento dessa avenida?

• A.

  3,3 Km.

• B.

  3,4 Km.

• C.

  3,5 Km.

• D.

  3,6 Km.

• E.

  3,8 Km.

Um vendedor ambulante vende empadas e coxinhas. Cada empada custa R$ 3,00 e cada coxinha custa R$ 2,00. Em um certo dia, ele vendeu 100 salgadinhos e arrecadou R$ 252,00. Quantas empadas ele vendeu nesse dia?

• A.

  46.

• B.

  48

• C.

  50.

• D.

  52.

• E.

  54.

Observe a seqüência de figuras planas abaixo, formada por palitos de fósforo.

Na figura formada por 135 palitos, existirão quantos triângulos como o da Figura-1?

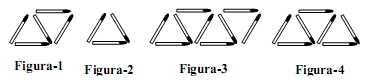
• A.

  59.

• B.

  60

• C.

  65.

• D.

  66.

• E.

  67

Considere as circunferências A, B, C e D abaixo, representadas em um sistema de coordenadas cartesianas:

No quadro abaixo, estão apresentadas as equações das quatro circunferências anteriores:

Associando cada circunferência à sua equação obtemos:

• A.

  A-1, B-2, C-3 e D-4.

• B.

  A-4, B-3, C-2 e D-1.

• C.

  A-1, B-3, C-2 e D-4.

• D.

  A-4, B-2, C-3 e D-1.

• E.

  A-2, B-3, C-4 e D-1.

Um relógio atrasa meio segundo a cada 20 minutos. Em dois dias ele atrasará:

• A.

  1 minuto e 4 segundos.

• B.

  1 minuto e 8 segundos.

• C.

  1 minuto e 12 segundos.

• D.

  1 minuto e 24 segundos.

• E.

  1 minuto e 30 segundos.

Às sete horas e vinte minutos, os ponteiros das horas e dos minutos de um relógio formam um ângulo que mede:

• A.

  90º;

• B.

  95º;

• C.

  100º;

• D.

  105º;

• E.

  110º.

Com um rolo de papel de parede é possível revestir 50 metros quadrados de parede. Para revestir as paredes de uma sala retangular com 8 metros de comprimento, 4 metros de largura e 3 metros de altura, sem descontar portas e janelas, gasta-se um rolo inteiro e mais uma parte do segundo rolo. Nessas condições, qual o percentual de papel de parede que sobra no segundo rolo?

• A.

  22%.

• B.

  44%.

• C.

  48%

• D.

  56%.

• E.

  72%.