Questões de Matemática da Núcleo de Computação Eletrônica UFRJ (NCE)

A tabela a seguir apresenta um resumo dos dados de transporte rodoviário coletivo interestadual e internacional de passageiros no Brasil em 2002.

Com base nesses dados, e considerando que todos os motoristas percorreram aproximadamente a mesma distância, podemos concluir que cada motorista percorreu, em 2002, a seguinte distância em quilômetros, aproximadamente:

• A.

  1.200.000;

• B.

  500.600;

• C.

  64.000;

• D.

  3.000;

• E.

  200.

A soma das raízes da equação do segundo grau: x² - 2x - 1 = 0 vale:

• A.

  -4

• B.

  -2

• C.

  0

• D.

  2

• E.

  4

As velocidades médias de 10 linhas de uma permissionária de transporte regular de passageiros se distribuem conforme o quadro a seguir.

• A. 42,5 km/h
• B. 44,0 km/h
• C. 47,0 km/h
• D. 50,0 km/h
• E. 53,0 km/h

Em uma receita para preparar 30 brigadeiros, são necessários uma lata de leite condensado, 200 g de chocolate em pó e meio tablete de margarina. Utilizando essa receita, e dispondo de 20 latas de leite condensado, 2600 g de chocolate em pó e 7 tabletes de margarina, o número máximo de brigadeiros que poderemos fazer é:

• A.

  600

• B.

  420

• C.

  400

• D.

  390

• E.

  320

Mediu-se a capacidade de um recipiente cujas dimensões foram dadas em centímetros e obteve-se como resposta 538 cm³. Essa medida é expressa em litros como:

• A.

  0,538

• B.

  5,38

• C.

  53,8

• D.

  538

• E.

  5380

As estimativas das tarifas de transporte rodoviário contratado podem em geral ser feitas a partir do ajuste de uma reta da variável independente Distância percorrida na variável dependente Tarifa, dado que, em geral, há uma dependência linear entre distância e tarifa praticada. Desse modo, a partir de um local, irradiam-se diferentes distâncias D e verificam-se as correspondentes tarifas T. Dada uma quantidade razoável de pares (Distância, Tarifa) observados, pode-se ajustar uma reta de regressão linear.

Suponha que, para um certo local, a reta ajustada da tarifa de transporte T em função da distância D apresente coeficiente linear igual a 5,10, coeficiente angular igual a 0,01, com um coeficiente de determinação de cerca de 90%. Nesse caso, para uma distância de 12km o modelo prevê uma tarifa de:

• A.

  3,85;

• B.

  4,40;

• C.

  5,12;

• D.

  6,54;

• E.

  7,55.

A fração que representa a dízima 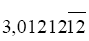 é:

• A.
• B.
• C.
• D.
• E.

Unem-se os pontos médios de um quadrado de lado 1 obtendo-se um novo quadrado. Unem-se então os pontos médios desse segundo quadrado obtendo-se um terceiro e, assim por diante, indefinidamente. A soma dos perímetros de todos esses quadrados é:

• A.

  

• B.

  

• C.
• D.
• E.

Considere uma progressão aritmética em que a₃ = 22 e a₉ = 6, o primeiro termo negativo é:

• A.

  a₁₁

• B.

  a₁₂

• C.

  a₁₃

• D.

  a₁₄

• E.

  a₁₅

Considere o gráfico da parábola da figura abaixo.

 A única equação que pode representar este gráfico é:

• A.

  y = x² + 3x;

• B.

  y = x² − 3x;

• C.

  y = x²;

• D.

  y = x² − 3;

• E.

  y = x² + 3;