Questões de Matemática da Fundação para o Vestibular da Universidade Estadual Paulista (VUNESP)

Para manter o forno aceso durante 7 horas diárias, uma pizzaria consome 49 m³ de lenha a cada 28 dias. Para um teste de mercado, os proprietários pretendem manter o forno aceso durante 10 horas diárias, por um período de 70 dias. Para a realização desse teste, a quantidade necessária de lenha será, em metros cúbicos, igual a

• A. 125.
• B. 137.
• C. 155.
• D. 170.
• E. 175.

A figura, com dimensões indicadas em centímetros, mostra uma placa informativa com o formato de um trapézio isósceles.

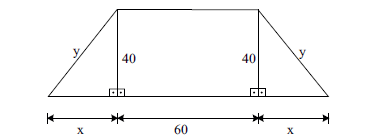
Se essa placa tem área de 3 600 cm², então o seu perímetro, em metros, é igual a

• A. 2,8.
• B. 2,6.
• C. 2,2.
• D. 2,0.
• E. 1,8.

Xavier e Yuri têm dívidas e pretendem pagá-las com o salário recebido. Sabe-se que 1/5 do valor da dívida de Xavier corresponde a 3/25 do valor da dívida de Yuri e que ambos, juntos, devem R$ 2.000,00. Desse modo, se Xavier pagar apenas 3/5 do valor total da sua dívida, ele ainda continuará devendo

• A. R$ 750,00.
• B. R$ 400,00.
• C. R$ 350,00.
• D. R$ 300,00.
• E. R$ 250,00.

Iniciando seu treinamento, dois ciclistas partem simultaneamente de um mesmo ponto de uma pista. Mantendo velocidades constantes, Lucas demora 18 minutos para completar cada volta, enquanto Daniel completa cada volta em 15 minutos. Sabe-se que às 9 h 10 min eles passaram juntos pelo ponto de partida pela primeira vez, desde o início do treinamento. Desse modo, é correto afirmar que às 8 h 25 min, Daniel já havia completado um número de voltas igual a

• A. 2.
• B. 3.
• C. 4.
• D. 5.
• E. 7.

Considere as sequências numéricas a e b, sendo que cada sequência obedece a um determinado padrão.

• A. 10.
• B. 9.
• C. 8.
• D. 6.
• E. 5.

Em uma placa retangular (ABCD) de alumínio foram desenhados, para posterior recorte, dois círculos, cujas circunferências são tangentes exteriores e tangenciam os lados da placa, conforme mostra a figura.

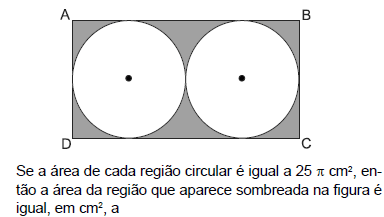
• A.
• B.
• C.
• D.
• E.

De acordo com a estratégia adotada para a corrida, um atleta percorreu os 2 km iniciais de certa prova com uma determinada velocidade constante. Em seguida, aumentou a velocidade imprimida no trecho inicial em 25% e, mantendo-a constante, percorreu os 4 km restantes e concluiu a prova. Se no primeiro trecho, ele gastou x minutos para percorrer 2 km, então o tempo total gasto para percorrer os 6 km da prova é corretamente expresso por

• A. 2,6 x.
• B. 2,25 x.
• C. 2 x.
• D. 1,6 x.
• E. 1,5 x.

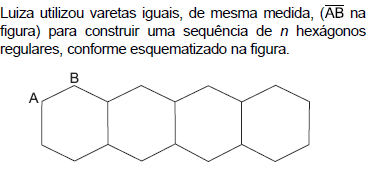
Sabe-se que ela tinha um total de 185 varetas, e que usou a quantidade necessária delas para construir o maior número possível de hexágonos. Nessas condições, é correto afirmar que o número n de hexágonos construídos, nessa sequência, e o número de varetas que restaram, após a construção, são, respectivamente,

• A. 30 e 3.
• B. 30 e 4.
• C. 35 e 4.
• D. 36 e 3.
• E. 36 e 4.

Três conjuntos, A, B e C, têm um total de 40 elementos. Sabe-se que 7 elementos pertencem apenas ao conjunto A, 10 elementos, apenas ao conjunto B, 13 elementos, apenas ao conjunto C, e pelo menos um elemento pertence simultaneamente aos três conjuntos. Os demais elementos podem pertencer ou a dois desses conjuntos ou aos três conjuntos. Desse modo, a maior diferença possível da quantidade total de elementos de certo conjunto em relação à quantidade total de elementos de outro conjunto é

• A. 4.
• B. 17.
• C. 6.
• D. 15.
• E. 27.

Porções iguais de 25 produtos similares foram testadas para determinar a quantidade exata de sódio por porção. Para a realização dos testes, os produtos foram divididos em dois grupos, A e B. Sabe-se que a média aritmética das quantidades de sódio encontradas nas porções do grupo A e do grupo B foram, respectivamente, de 100 mg e de 110 mg, e que a média aritmética das quantidades de sódio das 25 porções testadas foi de 104 mg. Desse modo, é correto afirmar que o número de produtos testados no grupo A era

• A. 18.
• B. 15.
• C. 12.
• D. 10.
• E. 9.