Questões de Pedagogia do ano 2004

Numa sala de aula de matemática, a professora cede a cada aluno três dados. Em seguida, pede que os enfileire e conte o número de faces. Passados alguns minutos, ela observou que havia três respostas: 11, 13 e 15. Numa análise com um grupo de professoras, chegou-se a construir três afirmativas:

 

Dentre essas afirmativas, pode-se dizer que

• A.

  todas estão corretas.

• B.

  somente a 2ª está correta.

• C.

  a 1ª e a 3ª estão corretas.

• D.

  a 2ª e a 3ª estão corretas.

• E.

  nenhuma está correta.

Vergnoud (1995), em Carraher, Carraher & Schliemann, no texto sobre "cultura matemática e modelos matemáticos", propõe uma abordagem sobre os estudos dos conceitos, apresentando nele três aspectos. Esses aspectos são

• A.

  objetivos-obstáculos; os invariantes e a questão da simbolização.

• B.

  conjunto de situações; os invariantes e a questão da simbolização.

• C.

  heurística; objetivos-obstáculos e os invariantes.

• D.

  heurística; os invariantes e os objetivos-obstáculos.

• E.

  conjunto de situações, os invariantes e os objetivos-obstáculos.

Numa sala de aula de matemática, a professora pergunta aos alunos: "Como é que vocês sabem que um número é maior do que outro?" Ouve, então, as respostas:

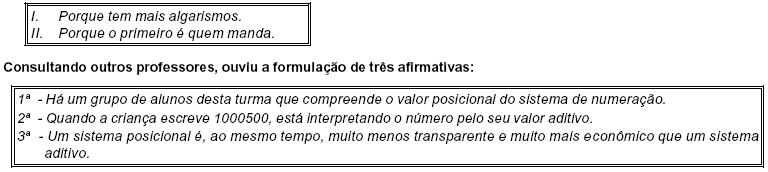
A professora conclui que

• A.

  todas as afirmativas estão corretas.

• B.

  somente a 2ª afirmativa está correta.

• C.

  somente a 3ª afirmativa está correta.

• D.

  as afirmativas 2ª e 3ª estão corretas.

• E.

  somente a 1ª afirmativa está correta.

Pergunta-se a uma criança quanto é 200 – 35. Ela responde: "se fosse 30 daria 70. Mas é 35, então é 65, 165". Este procedimento desenvolvido por ela

• A.

  está errado.

• B.

  é o de agrupamentos repetidos.

• C.

  é o da decomposição.

• D.

  estaria certo, se fosse para a operação 100–35.

• E.

  é do algoritmo do empréstimo.

Segundo o texto "Matemática escrita versus matemática oral" de Carraher, Carraher & Schliemann, é incorreto dizer que

• A.

  dados sobre as habilidades cognitivas dos alunos das escolas públicas e particulares, em geral, e matemática, em particular, mostraram diferenças significativas entre os dois grupos.

• B.

  as crianças entre 10-11 anos exercem uma atividade econômica, a qual faz com que a matemática elementar seja uma habilidade necessária à sobrevivência entre as crianças das classes populares nas cidades grandes.

• C.

  para o primeiro ano de aprendizagem formal da matemática, os resultados mostraram que 98% das crianças das escolas particulares foram aprovadas ao final do ano, contra apenas 68% das crianças das escolas públicas.

• D.

  este estudo mostrou que a diferença entre a eficiência das crianças na escola e na venda resulta das estratégias cognitivas escolhidas por elas para a resolução dos problemas.

• E.

  o procedimento oral era o preferido nas situações de venda e o procedimento escrito era o mais freqüente nos exercícios de computação.

Uma professora distribui cartões com a configuração de nove quadrados, conforme figura abaixo e um conjunto de dois pontos (fichas abaixo), denominado de constelações. A seguir, pede que os alunos preencham o quadro com as constelações (dois) de diversos modos possíveis para o quadrado dado, contando, em seguida, o número de possibilidades diferentes de preenchimentos.

Esta atividade didática/metodológica desenvolve

• A.

  a geometria métrica e a probabilidade, com 36 possibilidades diferentes, para se preencher o cartão com essa dada constelação.

• B.

  as representações de um número e a geometria formal, no sentido de informar apenas o nome da figura e as possibilidades, que são de 49 modos possíveis, para se preencher o cartão com essa dada constelação.

• C.

  a noção de espaço e as possibilidades, que são de 36 modos diferentes, para se preencher o cartão com essa dada constelação.

• D.

  as representações de um número e a geometria formal, no sentido de informar, apenas, o nome da figura e as possibilidades, que são de 36 modos possíveis, para se preencher o cartão com essa dada constelação.

• E.

  a geometria métrica e a probabilidade com 49 possibilidades diferentes, para se preencher o cartão com essa dada constelação.

Uma professora, na sala de aula da quarta série do ensino fundamental, propõe que seus alunos resolvam a operação 13 : 4. Ao analisar as respostas de seus alunos, comenta com outros professores que obteve respostas onde: ora o quociente era 3 e resto 2; ora o quociente era 3,52 e o resto 0. Diante disto, ouviu os seguintes comentários:

Deste modo, está(ão) correta(s) a(s) professora(s)

• A.

  X, Y e Z.

• B.

  Y e Z.

• C.

  X apenas.

• D.

  X e Y apenas.

• E.

  Y apenas.

Para Parra, no artigo "cálculo mental na escola primária" (em Parra e Saiz), ela pleiteia o melhoramento da contagem em duas direções. E, numa delas, refere-se ao que diz respeito ao domínio e à extensão da série numérica oral. Nesse sentido, cita algumas capacidades que o aluno deve dispor da série numérica oral para o cálculo mental. Leia as afirmativas abaixo.

Dentre essas capacidades citadas, segundo a autora, estão corretas as afirmativas

• A.

  I e II.

• B.

  II e III.

• C.

  I, II e III.

• D.

  II, III e IV.

• E.

  I, II, III e IV.

Para Brousseau, em Parra e Saiz, o objeto de estudo da didática da matemática é a situação didática. E, para análise das situações didáticas, Brousseau distingue quatro tipos nos processos didáticos, e dentre eles, apenas um, dentre as opções abaixo, não faz parte deste contexto. Assinale-o.

• A.

  Situações de ação.

• B.

  Situações de obstáculos.

• C.

  Situações de formulações.

• D.

  Situações de validação.

• E.

  Situações de institucionalização.

Para Brousseau, em Parra e Saiz, a escolha das condições de ensino se justifica, exclusivamente, pela necessidade de dar sentido aos conhecimentos, e, para isso, descreve quatro características que dão sentido aos conhecimentos. Sabendo disto, assinale a alternativa que não corresponde a um desses quatro sentidos.

• A.

  Modelos "incitativos".

• B.

  Tramas de raciocínios e provas.

• C.

  Trama de reformulações e formulações.

• D.

  Modelos implícitos.

• E.

  Relações essencialmente dialéticas.