Questões de Estatística do ano 2011

Considere uma distribuição conjunta de probabilidades, contínua e uniforme sobre o quadrado hachureado do gráfico abaixo, definido pelos intervalos nos eixos:

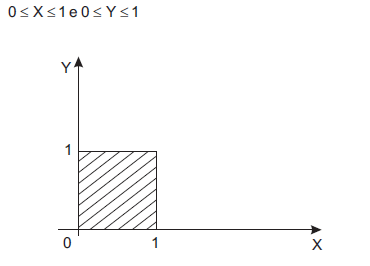
• A.

  0.7

• B.

  0.6

• C.

  0.5

• D.

  0.4

• E.

  0.3

Considere uma distribuição conjunta de probabilidades, contínua e uniforme sobre o círculo de raio 1, centrado no ponto (1, 1), como mostra o gráfico abaixo. O gráfico também mostra dois outros círculos, A e B, centrados em (1, 1) e com raios de 0,25 e 0,5, respectivamente.

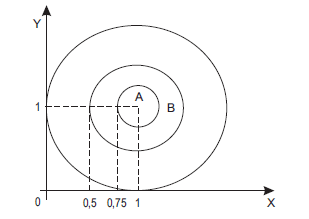
A probabilidade de que um ponto (X, Y) pertença a A, dado que pertence a B, é

• A.

  3/5

• B.

  1/2

• C.

  1/3

• D.

  1/4

• E.

  1/5

Quando se lança uma certa moeda, a probabilidade de o resultado ser cara é p. A moeda foi lançada dez vezes, sucessivas e independentes, e o resultado foi de 2 caras e 8 coroas. Tendo em vista este experimento, a estimativa de máxima verossimilhança de p é

• A.

  0.2

• B.

  0.25

• C.

  0.3

• D.

  0.35

• E.

  0.4

A probabilidade de que ocorra o evento X, dado que o evento Y ocorreu, é positiva e representada por P(X/Y). Similarmente, a probabilidade de que ocorra Y, dado que X ocorreu, é representada por P(Y/X). Se P(X/Y) = P(Y/X), os eventos X e Y são

• A.

  ortogonais

• B.

  coincidentes

• C.

  independentes

• D.

  igualmente prováveis>

• E.

  mutuamente exclusivos

Uma distribuição de probabilidades simétrica, com forma de sino e definida a partir de um único parâmetro v, denominado graus de liberdade, é uma distribuição:

• A.

  normal.

• B.

  lognormal.

• C.

  qui-quadrado.

• D.

  t de Student.

• E.

  F de Fisher-Snedecor.

Uma pessoa lança repetidamente um dado equilibrado, parando quando obtém a face com o número 6. A probabilidade de que o dado seja lançado exatamente 3 vezes é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

• A.

  1/4

• B.

  1/3

• C.

  5/16

• D.

  3/8

• E.

  1/2

Seja (X,Y) uma variável aleatória bidimensional distribuída uniformemente sobre a região R = {y > 0, 0 < x < 1, x + y < 1}. A probabilidade P(Y < 3X) vale

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Sejam X e Y duas variáveis aleatórias contínuas, com funções de densidade marginais f_X(x) e f_Y(y), respectivamente, e função de densidade conjunta f_X,Y(x,y). As variáveis X e Y são independentes se

• A.

  f_X,Y(x,y) = f_X(x) f_Y(y)

• B.

  f_X,Y(x,y) = 0

• C.

  E(XY) = E(X)E(Y)

• D.

  X e Y têm distribuições normais

• E.

  a correlação entre X e Y é igual a zero