Questões de Estatística da Escola de Administração Fazendária (ESAF)

Selecione a opção que apresenta corretamente o significado de amostra.

• A.

  Coleta de dados realizada no conjunto de todos os elementos do universo da população.

• B.

  Técnica de coleta de dados.

• C.

  Forma de tratamento dos dados coletados.

• D.

  Parte de dada população escolhida para realização de uma pesquisa.

• E.

  Seqüência de atividades destinadas à coleta de dados.

Em uma distribuição de sinistro S, formulando-se a hipótese de que não há diferença entre a freqüência esperada e a observada (hipótese nula: Ho). Donde, segundo um determinado nível de significância, podemos afirmar que ocorreu

• A. um erro do tipo I, se for aceita a hipótese Ho.
• B. um erro do tipo II, se for rejeitada a hipótese Ho.
• C. um erro do tipo I, se for aceita a hipótese Ho, sendo esta correta.
• D. um erro do tipo II, se for rejeitada a hipótese Ho, sendo esta correta.
• E. um erro do tipo I, se for rejeitada a hipótese Ho, sendo esta correta.

O modelo ARMA é um modelo

• A.

  não estacionário.

• B.

  estacionário.

• C.

  não estacionário, exclusivamente auto-regressivo.

• D.

  sazonal.

• E.

  estacionário, exclusivamente de média móvel.

Sobre o modelo SARIMA em relação ao modelo ARIMA pode-se afirmar que

• A.

  a eventual sazonalidade do modelo é remota, mantendo-o, na maioria das vezes, nesta forma mais simples de formulação.

• B.

  passa a considerar a variável sazonalidade na estruturação do modelo, tornando-se mais complexo, ao trabalhar com mais variáveis.

• C.

  ao introduzir variáveis do tipo Qui-quadrado, torna o modelo mais complexo, pois trabalha com mais variáveis.

• D.

  ao introduzir variáveis do tipo Log-normal, torna o modelo mais complexo, pois trabalha com mais variáveis.

• E.

  ao introduzir variáveis do tipo Binomial, torna o modelo mais complexo, pois trabalha com mais variáveis.

Os eventos E₁ e E₂ são os conjuntos de pontos que podem estar tanto em E₁ quanto em E₂, como em ambos, simultaneamente. Então, a probabilidade de uma ocorrência ser do evento E₁ ou E₂ é dada por:

• A. (E₁ + E₂) = P(E₁) + P(E₂).
• B. P (E₁ + E₂) = P(E₁) + P(E₂) - P (E₁ E₂).
• C. P (E₁ + E₂) = P(E₁) + (1 - P(E₂).
• D. P (E₁ + E₂) = P(E₂) + (1 - P(E₁)).
• E. P (E₁ + E₂) = P(E₁) * P(E₂).

Um grupo de 1.000 pessoas tem a seguinte composição etária (em anos):

 - [ 0 - 20]: 200 pessoas;

 - [21 - 30]: 200 pessoas;

- [31 - 40]: 200 pessoas;

 - [41 - 50]: 200 pessoas;

 - de 51 anos em diante: 200 pessoas.

Considerando que as probabilidades média de morte (qx), segundo uma determinada tábua, é de:

 - [0 - 20] até 20 anos: 0,600% o (por mil);

- [21 - 30]: 0,800%o (por mil);

 - [31 - 40]: 1,500%o (por mil);

 - [41 - 50]: 5,000%o (por mil);

- de 51 anos em diante: 20,000% o (por mil).

 Pode-se afirmar que a possibilidade de ocorrer a morte de exatamente 10 pessoas com idade superior a 51 anos é um evento:

• A. Certo.
• B. Impossível.
• C. Provável.
• D. Muito Provável.
• E. Pouco Provável.

Se p é a probabilidade de um evento acontecer em uma tentativa única e seu complemento (1 – p) é a probabilidade do evento não ocorrer (distribuição binomial), então a probabilidade do evento ocorrer exatamente X vezes, em n tentativas é dada por:

• A. p(X) = _nC_X p^X q^n-X
• B. p(X) = 1 - p^X q^n-X
• C. p(X) = p^X q^n-X
• D. p(X) = 1 + _nC_X p^X q^n-X
• E. p(X) = p^X - q^n-X

Se a variável X pode assumir um conjunto infinito (contínuo) de valores, o polígono de freqüência relativa de uma amostra torna-se uma curva contínua, cuja equação é Y = p(X). A área total limitada por essa curva e pelo eixo dos X é igual a 1 e a área compreendida entre as verticais X = a e X = b, sendo a < b e, ambos, contidos na área total da curva, a probabilidade de X cair neste intervalo a e b é dada por:

• A.

  <X

• B.
• C. P (a>X>b), composta pela soma de P(X=a) – P(X=b).
• D. P (a>X>b), composta pela integral de P(X=a) até P(X=b).
• E.

Seja X₁, X₂, ... uma sucessão de variáveis aleatórias identicamente distribuídas, cada uma com média 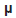 e variância ¶², tendo a propriedade de que qualquer número finito delas são independentes. Então, para cada z

onde Þ(z) é uma função de distribuição:

• A. Normal reduzida.
• B. Normal.
• C. Qui-quadrado.
• D. Log-normal.
• E. Binomial.

Considerando V = Verdadeiro e F = Falso e o contido em cada item abaixo, qual é a opção que indica as respostas com as alternativas adequadas (para cada item e com base em todo o texto do respectivo item):

( ) Nas curvas de freqüência simétrica ou em forma de sino caracterizam-se pelo fato das observações eqüidistantes do ponto central máximo terem a mesma freqüência.

( ) Nas curvas de moderadamente assimétrica ou desviadas, a cauda da curva de um lado da ordenada máxima é mais longa do que do outro lado. Se o ramo mais alongado fica à direita, a curva é dita desviada para a direita ou de assimetria negativa, enquanto que, se ocorrer o inverso, diz-se que a curva é desviada para a esquerda ou de assimetria positiva.

( ) Nas curvas em forma de J (letra jota ou anzol) ou J invertido, o ponto de ordenada máxima ocorre em uma das extremidades.

• A. V, F, F
• B. V, V, F
• C. V, F, V
• D. F, V, F
• E. F, F, V