Questões de Estatística da Escola de Administração Fazendária (ESAF)

Na análise da sinistralidade de uma determinada carteira, uma medida de discrepância existente entre as freqüências observadas e as esperadas é proporcionada pela estatística quí quadrado - X² . Com base nisso, pode-se afirmar que se:

• A. X² = 0, as freqüências teóricas (esperadas) e as observadas concordam exatamente.
• B. X² = 0, as freqüências teóricas (esperadas) e as observadas não concordam exatamente nem parcialmente.
• C. X² = 0, as freqüências teóricas (esperadas) e as observadas concordam parcialmente, pode ser aceita-se como tal.
• D. X² = 1, as freqüências teóricas(esperadas) e as observadas concordam exatamente.
• E. X² ¡Ù 0, as freqüências teóricas (esperadas) e as observadas concordam exatamente.

Em uma população bastante grande, observou-se uma média igual a 50 e desvio-padrão igual a 12. Com essas informações, pode-se afirmar que a distribuição de amostragem da média das amostras de tamanho n = 36, apresenta expectância e desvio-padrão, respectivamente, iguais a

• A.

  50 e 12.

• B.

  50 e 2.

• C.

  25 e 12.

• D.

  25 e 6.

• E.

  25 e 3.

Sendo qx a probabilidade de uma pessoa de idade "x" falecer nesta idade "x" e qy a probalidade de uma pessoa de idade "y" falecer nesta idade "y" e px = (1 - qx) e py = (1 - qy), pode-se afi rmar que o resultado da equação [1 - px py] indica:

• a.

  a probabilidade de ambos vivos.

• b.

  a probabilidade de pelo menos um vivo.

• c.

  a probabilidade de pelo menos um morto.

• d.

  a probabilidade de ambos mortos.

• e.

  a probabilidade de "x" vivo e "y" morto ou "y" vivo e "x" vivo.

No campo estatístico, ogivas são:

• a.

  polígonos de freqüência acumulada.

• b.

  polígonos de freqüência acumulada relativa ou percentual.

• c.

  histograma de distribuição de freqüência.

• d.

  histograma de distribuição de freqüência relativa ou percentual.

• e.

  o equivalente à amplitude do intervalo.

No estudo da Estatística Descritiva serão considerados como pequenos os conjuntos de dados que contenham até 30 elementos ou como grandes quando o conjunto de dados possuir mais de 30 elementos. Este parâmetro de 30 elementos é um referencial que, muito embora indicado e utilizado com muita freqüência, depende da situação e peculiaridades da variável em estudo.

Para um (1) conjunto de dados de qualquer tamanho de uma variável, as suas informações podem ser resumidas estatisticamente de acordo com as seguintes medidas:

Indique a opção falsa.

• A.

  Medidas de tendência central ou posição.

• B.

  Medidas de dispersão ou variabilidade.

• C.

  Medidas de assimetria.

• D.

  Medidas de achatamento ou curtose.

• E.

  Medidas de correlação.

Histograma e Polígono de freqüência são

• a.

  a mesma representação gráfica (idênticas) de uma distribuição de freqüência.

• b.

  um texto descritivo e uma representação gráfica de uma distribuição de freqüência.

• c.

  um texto descritivo e uma função gráfica de uma distribuição de freqüência.

• d.

  duas representações gráficas de uma distribuição de freqüência.

• e.

  duas representações gráficas de uma distribuição de freqüência, porém com sentidos opostos.

Considere a seguinte distribuição de idades, em anos, referentes a 180 crianças. Os intervalos são fechados à esquerda e abertos à direita:

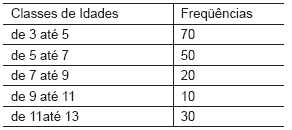
Sobre essa distribuição de idades, é correto afirmar que

• A.

  a idade mediana encontra-se na classe de 7 até 9.

• B.

  a idade modal encontra-se na classe de 5 até 7.

• C.

  a idade modal encontra-se na classe de 7 até 9.

• D.

  a idade modal encontra-se na classe de 9 até 11.

• E.

  a idade modal encontra-se na classe de 3 até 5.

O conjunto de notas dos alunos de uma determinada prova é: {10, 5, 3, 4, 5, 10, 3, 8, 9, 3}. Assim, podemos dizer que a moda, média e mediana deste conjunto são, respectivamente:

• A.

  3, 6 e 5.

• B.

  3, 4 e 5.

• C.

  10, 6 e 5.

• D.

  5, 4 e 3.

• E.

  3, 6 e 10.

A média aritmética entre as idades de Ana, Amanda, Clara e Carlos é igual a 16 anos. As idades de Ana e Amanda são, respectivamente, iguais a seis e oito anos. Paulo, primo de Ana, é quatro anos mais novo do que Carlos. Jorge, irmão de Amanda, é oito anos mais velho do que Clara. Assim, a média aritmética entre as idades de Jorge e Paulo é, em anos, igual a

• A.

  20.

• B.

  13.

• C.

  24.

• D.

  27.

• E.

  38.

Seja X uma variável aleatória com distribuição normal padrão. Sabe-se que a probabilidade de X ser maior do que 1,96 desvio padrão é igual a 2,5%. Desse modo, se Y é uma variável normal com média 10 e variância 4, então a probabilidade de Y ser maior do que 6,08 e menor do que 10 é igual a

• a.

  97,5 %.

• b.

  95 %.

• c.

  47,5%.

• d.

  5 %.

• e.

  90 %.