Questões de Estatística da Escola de Administração Fazendária (ESAF)

Uma variável aleatória contínua, x, tem função densidade de probabilidade igual a: f(x) = 2x, para 0 < x < 1 e f(x) = 0 para qualquer outro valor de x que estiver fora deste intervalo. Assim, pode-se afirmar que

• A.

  P (0< x < 0,2) = 0,2

• B.

  P (0< x < 0,2) = 0,4

• C.

  P (0< x < 0,2) = 0,24

• D.

  P (0< x < 0,2) = 0,06

• E.

  P (0< x < 0,2) = 0,04

Considere os seguintes conjuntos de observações referentes a cinco diferentes variáveis:

A { 1; 1; 1; 1; 1; 50},

B {1, 1, 1, 1; 50; 50},

C {1, 1, 1, 50, 50, 50 },

D {1, 1, 50, 50, 50, 50 },

E {1, 50, 50, 50, 50, 50}.

O conjunto de observações que apresenta a maior variabilidade, medida pelo desvio-padrão, é o referente à variável

• A.

  A.

• B.

  B.

• C.

  E.

• D.

  D.

• E.

  C.

A "Lei dos Grandes Números" estabelece que à medida que aumenta o número de vezes, n, que se repete um experimento probabilístico, tem-se que

• A.

  a probabilidade teórica da ocorrência de um evento tende para sua freqüência absoluta, se n > 10.

• B.

  a freqüência absoluta de um evento tende para a sua probabilidade teórica, se n > 30.

• C.

  a freqüência relativa de um evento tende para o desvio relativo do evento, se n > 100.

• D.

  freqüência relativa de um evento tende para sua probabilidade teórica, se n for suficientemente grande.

• E.

  a freqüência relativa de um evento tende para sua probabilidade teórica, independente de n.

Qual a variação (índice de aumento ou redução) do preço médio verificado na tabela de compras abaixo?

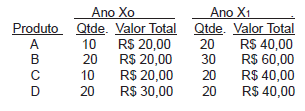
• A.

  25%.

• B.

  33%.

• C.

  50%.

• D.

  125%.

• E.

  133%

Tendo que a sinistralidade (S) de uma carteira de automóveis de "n" observações foi avaliada em função das variáveis: X, relativa ao modelo do veículo, e Y, perfil do condutor, resultando os pontos: (X₁, Y₁, S₁), (X₂, Y₂, S₂), ..., (X_n, Y_n, S_n), podendo S ser descrita pela expressão:

 S = a₀ + a₁X + a₂Y.

 Avaliando S em função de valores atribuídos a X e Y, falando- se de um plano de mínimo quadrado de ajustamento de dados, as equações normais correspondentes ao plano de mínimo quadrado são dadas por:

Indicando por V – Verdadeiro e F – Falso, temos a opção correta como sendo:

• A. V, F, F
• B. V, V, F
• C. V, F, V
• D. F, V, F
• E. F, F, V

Uma escola aplicou a mesma prova para duas turmas de alunos: turma T₁ e turma T₂. Como de praxe, quanto maior a nota obtida, melhor será considerado o desempenho do aluno. Sabe-se que a nota média da turma T1 foi igual a 75, a nota média da turma T₂ foi igual a 70. Sabe-se, também, que a variância das notas é igual a 16 para as duas turmas. Fernando, que realizou o teste na turma T₁, obteve nota igual a 75. Flávia, que realizou o teste na turma T₂ obteve nota igual a 70. Deste modo pode-se concluir que:

• a.

  Fernando e Flávia apresentaram o mesmo desempenho absoluto.

• b.

  Fernando e Flávia apresentaram o mesmo desempenho relativo.

• c.

  o desempenho absoluto de Fernando foi menor do que o de Flávia.

• d.

  o desempenho relativo de Flávia foi maior do que o de Fernando.

• e.

  o desempenho relativo de Fernando foi maior do que o de Flávia.

• A.

  �� = 1 - ��.

• B.

  �� é o nível de significância do teste.

• C.

  só se comete Erro Tipo I quando a amostra tiver menos do que 30 observações.

• D.

  só se comete Erro Tipo II quando a amostra tiver menos do que 30 observações.

• E.

  a probabilidade de não se cometer erro algum em um teste é igual a ��.

Sabe-se que x₁, x₂ e x₃ representam, respectivamente, o primeiro, segundo e terceiro elemento de uma amostra de tamanho três, retirada de uma população com média μ e variância σ2. Sabe-se, também, que A e B são estimadores da média populacional, onde A = 3/4 x₁ + 1/8 x₂ + 1/8 x₃ e B = 3/4 x₁ + 1/8 x₂. Com essas informações tem-se que

• A.

  A é estimador não-tendencioso e variância de A é igual a 0,5 σ².

• B.

  A é estimador não-tendencioso e B é estimador tendencioso.

• C.

  B é estimador não-tendencioso e variância de B é igual a 0,5 σ².

• D.

  B é estimador tendencioso e variância de B é igual à variância de A.

• E.

  A e B são estimadores tendenciosos e possuem a mesma variância.

Considerando o coeficiente de curtose das distribuições de probabilidade, pode-se afirmar que a seqüência que apresenta ordem crescente com relação à respectiva dispersão dos dados é dada pelas distribuições

• A.

  leptocúrtica, mesocúrtica e platicúrtica.

• B.

  platicúrtica, mesocúrtica e leptocúrtica.

• C.

  platicúrtica, leptocúrtica e mesocúrtica.

• D.

  leptocúrtica, platicúrtica e mesocúrtica.

• E.

  mesocúrtica, leptocúrtica e platicúrtica.

Uma empresa aplicou o mesmo teste de desempenho para determinada função a dois diferentes grupos de funcionários: o grupo A e o grupo B. Nesse teste, quanto maior o número de pontos atingidos, melhor é o desempenho do funcionário. Sabe-se que a média de pontos alcançada pelo grupo A foi igual a 75, com desvio-padrão 5. Sabe-se, também, que a média de pontos alcançada pelo grupo B foi igual a 70, com variância 100. Carlos, que participou do grupo A, obteve 85 pontos. Maria, que participou do grupo B, obteve 80 pontos. Assim, pode-se afirmar que

• A.

  o desempenho relativo de Carlos foi pior do que o de Maria.

• B.

  ambos tiveram o mesmo desempenho relativo.

• C.

  o desempenho relativo de Carlos foi melhor do que o de Maria.

• D.

  o desempenho de Maria apresentou maior variabilidade.

• E.

  o desempenho de Carlos apresentou menor variabilidade.