Questões de Estatística da Escola de Administração Fazendária (ESAF)

Considere a seguinte distribuição de idades, dadas em anos, referente a 30 alunos de uma escola. Sabendo-se que os intervalos são fechados à esquerda e abertos à direita, então os valores da idade mediana e da idade média são, respectivamente iguais a:

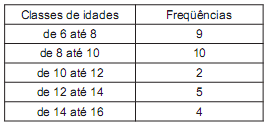
• a.

  9,2 anos e 11 anos

• b.

  10 anos e 10,2 anos

• c.

  10 anos e 11 anos

• d.

  11 anos e 10,2 anos

• e.

  9,2 anos e 10 anos

Em uma distribuição positivamente assimétrica, tem-se que

• A.

  a média é maior do que a moda, e a moda maior do que a mediana.

• B.

  a moda é maior do que a mediana, e a mediana maior do que a média.

• C.

  a moda é maior do que a média, e a média maior do que a mediana.

• D.

  a mediana é maior do que a moda, e a moda maior do que média.

• E.

  a média é maior do que a mediana, e a mediana maior do que a moda.

O valor mais próximo da média harmônica do conjunto de dados: {10, 5, 3, 4, 5, 10, 3, 8, 9, 3} é igual a

• A.

  6.

• B.

  6,5.

• C.

  4,794.

• D.

  10.

• E.

  3,9.

Sendo X uma v. a. d. – variável aleatória discreta e sendo Y = aX + b, pode concluir-se que var (aX + b) é igual a:

• A. = var X.
• B. = E(X²) – (EX)².
• C. = E(X – E(X) ².
• D. = a² var X.
• E. = a² var X – b.

Sabe-se que X e Y são variáveis aleatórias independentes. Dado que Z = 2 X – Y, então pode-se afi rmar que

• A.

  a variância de Z nunca poderá ser superior à variância de X.

• B.

  a variância de Z nunca poderá ser inferior à variância de Y.

• C.

  a variância de Z poderá se diferente de 2 X - Y.

• D.

  o valor esperado de Z é igual a 2.

• E.

  a variância de Z é igual a zero.

A média aritmética discreta de uma população qualquer é dada pela seguinte formulação:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Indicando por:

E desde que todos os valores da amostra sejam positivos e diferentes entre si, é verdadeiro afi rmar que a relação entre estas médias é:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

• A.

  

• B.

  

• C.

  

• D.

  30

• E.

  

Sabe-se que a probabilidade de uma variável, com distribuição normal com média zero e variância igual a um, estar no intervalo (μ ± 1,64 σ) é igual a 90%. Uma amostra de tamanho 144 forneceu os valores 20 e 36 para as estimativas da média e da variância populacional, respectivamente. Assim, o intervalo com 90% de confi ança para a média desta população é dado por

• A.

  

• B.

  µ ± 1,64x6

• C.

  

• D.

  µ ± 1,64x12

• E.

  µ ± 1,64x36

Sendo a moda menor que a mediana e, esta, menor que média, pode-se afirmar que se trata de uma curva

• a.

  Simétrica.

• b.

  Assimétrica, com freqüências desviadas para a direita.

• c.

  Assimétrica, com freqüências desviadas para a esquerda.

• d.

  Simétrica, com freqüências desviadas para a direita.

• e.

  Simétrica, com freqüências desviadas para a esquerda.